
【题目】如图,设△ABC的两边AC与BC之和为a,M是AB的中点,MC=MA=5,则a的取值范围是_____.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】一个多边形的所有内角与它的一个外角之和是2018°,求这个外角的度数和它的边数.
【答案】38° ; 边数13
【解析】试题分析:根据多边形的内角和公式(n-2)180°可知,多边形的内角和是180°的倍数,然后列式求解即可.
试题解析:设多边形的边数是n,加的外角为α,则
(n-2)180°+α=2018°,
α=2378°-180°n,又0<α<180°,
即0<2378°-180°n<180°,
解得: ![]() <n<
<n<![]() ,
,
又n为正整数,
可得n=13,
此时α=38°满足条件,
答:这个外角的度数是38°,它的13边形.
【点睛】本题考查了多边形的内角和公式,利用好多边形的内角和是180°的倍数是解题的关键.
【题型】解答题
【结束】
22
【题目】已知![]() , 求 (1)
, 求 (1) ![]() ; (2)
; (2) ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
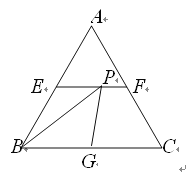
【题目】如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、
AC、BC的中点,点P为线段EF上一个动点,连接BP、GP,则△BPG的周长的最小值是
_ ▲ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+4x+c与y轴交于点A(0,5),与x轴交于点E,B,点B坐标为(5,0).
(1)求二次函数解析式及顶点坐标;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知坐标原点为![]() ,点
,点![]() ,将
,将![]() 绕原点
绕原点![]() 顺时针旋转
顺时针旋转![]() 后,
后,![]() 的对应点
的对应点![]() 的坐标是( )
的坐标是( )
A. (2,-1) B. (-2,1) C. (1,-2) D. (-1,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.

(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线l1与x轴、y轴分别交于点A(3,0)、B(0,2).
(1)如图2,点M是AB的中点,过点M作ME⊥x轴,MF⊥y轴,垂足分别为E、F.则点M 的坐标为 ;
(2)如图3,直线l2经过点B,且与l1互相垂直,过点C(0,﹣1)作CD⊥y轴,交l2于点D.则以直线l2为图像的函数表达式为 ;
(3)图1中,在x轴上是否存在点P,使得△APB是等腰三角形.如果存在,请求出点P的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.
(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;
(2)按照(1)中收到捐款的增长速度,第四天该单位能收到多少捐款?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com