
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 交于
交于![]() 点,且
点,且![]() ,点
,点![]() 是
是![]() 轴上的一个动点,当
轴上的一个动点,当![]() 的值最小时,
的值最小时,![]() 的值是( )
的值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
作出点C关于x轴的对称点C′,连接C′D交x轴于点M,根据轴对称性及两点之间线段最短可知此时CM+DM最小;
由ED∥y轴得到△C′OM∽△DEM,进而得到![]() =
=![]() ,将各线段的长代入该式进行求解即可.
,将各线段的长代入该式进行求解即可.
∵点A(-1,0)在抛物线y=![]() x2+bx-2上,
x2+bx-2上,
∴![]() ×(-1)2+b×(-1)-2=0.
×(-1)2+b×(-1)-2=0.
解得b=-![]() .
.
∴抛物线的解析式为:y=![]() x2-
x2-![]() x-2,
x-2,
配方得:y=![]() (x-
(x-![]() )2-
)2-![]() ,
,
∴顶点D的坐标为(![]() ,-
,-![]() ).
).
作出点C关于x轴的对称点C′,则C′(0,2),OC′=2,连接C′D交x轴于点M,

根据轴对称性及两点之间线段最短,可知CM+DM的值最小.
∵ED∥y轴,
∴△C′OM∽△DEM,
∴![]() =
=![]() .
.
∵OM=m,EM=![]() -m,OC′=2,ED=
-m,OC′=2,ED=![]() ,
,![]() =
=![]() ,
,
∴![]() =
=![]() .
.
解得m=![]() .
.
故答案选B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】将一块直角三角板DEF放置在锐角△ABC上,使得该三角板的两条直角边DE、DF恰好分别经过点B、C.

(1)如图①,若∠A=40°时,点D在△ABC内,则∠ABC+∠ACB= 度,∠DBC+∠DCB= 度,∠ABD+∠ACD= 度;
(2)如图②,改变直角三角板DEF的位置,使点D在△ABC内,请探究∠ABD+∠ACD与∠A之间存在怎样的数量关系,并验证你的结论.
(3)如图③,改变直角三角板DEF的位置,使点D在△ABC外,且在AB边的左侧,直接写出∠ABD、∠ACD、∠A三者之间存在的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有点E,且EF=ED.
(1)求证:DE是⊙O的切线;
(2)若tanA=![]() ,探究线段AB和BE之间的数量关系,并证明;
,探究线段AB和BE之间的数量关系,并证明;
(3)在(2)的条件下,若OF=1,求圆O的半径.
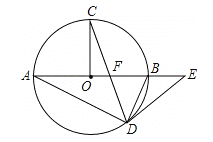
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OC是∠AOB的角平分线,P是OC上一点,PD⊥OA,PE⊥OB,垂足分别为D,E.F是OC上另一点,连接DF,EF.求证:DF=EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 放置在平面直角坐标系中,
放置在平面直角坐标系中,![]() ,
,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,反比例函数
轴,反比例函数![]() 的图象经过
的图象经过![]() 的中点
的中点![]() ,并且与
,并且与![]() 交于点
交于点![]() ,已知
,已知![]() .则
.则![]() 的长等于( )
的长等于( )

A. 2.5 B. 2 C. 1.5 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点![]() ,
,![]() 及原点
及原点![]() ,顶点为
,顶点为![]() .
.

(1)求抛物线的解析式:
(2)试判断![]() 的形式,并说明理由:
的形式,并说明理由:
(3)![]() 是抛物线上第二象限内的动点,过点
是抛物线上第二象限内的动点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,是否存在点
,是否存在点![]() 使得以点
使得以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,求出点
相似?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京广高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的![]() ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.4万元,乙队每天的施工费用为5.6万元.工程预算的施工费用为500万元.为缩短工期并高效完成工程,拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:
①∠CEG=2∠DCB;②∠DFB=![]() ∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正确的个数是( )
∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com