

| 112.5 |
| 25 |
| 292.5 |
| 25 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图,已知A、B是线段EF上两点,EA:AB:BF=1:2:3,M、N分别为EA、BF的中点,且MN=8cm,则EF长( )
如图,已知A、B是线段EF上两点,EA:AB:BF=1:2:3,M、N分别为EA、BF的中点,且MN=8cm,则EF长( )| A、9cm | B、10cm |
| C、11cm | D、12cm |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 销售方式 | 批发 | 零售 | 储藏后销售 |
| 售价(元/吨) | 3000 | 4500 | 5500 |
| 成本(元/吨) | 700 | 1000 | 1200 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,身高1.6米的小明从距路灯的底部(点O)20米的点A沿AO方向行走14米到点C处,小明在A处,头顶B在路灯投影下形成的影子在M处.
如图,身高1.6米的小明从距路灯的底部(点O)20米的点A沿AO方向行走14米到点C处,小明在A处,头顶B在路灯投影下形成的影子在M处.查看答案和解析>>
科目:初中数学 来源: 题型:
| 甲种客车 | 乙种客车 | |
| 载客量(人/辆) | 45 | 30 |
| 租金(元/辆) | 400 | 280 |
查看答案和解析>>
科目:初中数学 来源: 题型:
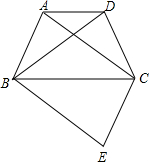 如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.
如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.查看答案和解析>>
科目:初中数学 来源: 题型:
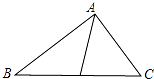 阅读理解
阅读理解| AB |
| BD |
| AC |
| CD |
| AB |
| BD |
| AC |
| CD |
| AB |
| BD |
| AC |
| CD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com