6
分析:根据折叠的性质得出CF=HF,BE=GE,设BE=GE=x,则AE=4-x,再利用勾股定理首先求出BE的长,即可得出AE,利用角相等三角函数值就相等,即可求出CF,即可得出答案.
解答:
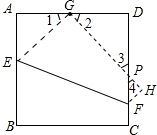
解:由题意,点C与点H,
点B与点G分别关于直线EF对称,
∴CF=HF,BE=GE.
设BE=GE=x,则AE=4-x.
∵四边形ABCD是正方形,
∴∠A=90°.
∴AE
2+AG
2=EG
2.
∵B落在边AD的中点G处,
∴AG=2,
∴(4-x)
2+2
2=x
2.
解得x=2.5.
∴BE=2.5.
∵四边形ABCD是正方形,
∴AB∥CD,∠B=90°.
∵点E,F分别在AB,CD边上,
∴四边形BCFE是直角梯形.
∵BE=GE=2.5,AB=4,
∴AE=1.5.
∴sin∠1=

,tan∠1=

.
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠3=∠1.
∴sin∠3=sin∠1=

,
在Rt△DGP中,∵∠D=90°,
DG=2,sin∠3=
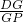
=

,
∴PG=

,
∴PH=GH-GP=

,
∵∠4=∠3,
∴tan∠4=tan∠3=tan∠1=

,
在Rt△HPF中,∵∠H=∠C=90°,
∴FC=HF=

.
∴S
四边形BCFE=

(FC+BE)×BC=

×(

+2.5)×4=6.
故答案为:6.
点评:此题主要考查了折叠问题与解直角三角形以及正方形的知识,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,以及解直角三角形时相等的角三角函数值相等.

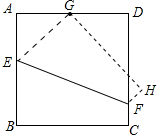 如图,将边长为4的正方形ABCD沿着折痕EF折叠,使点B落在边AD的中点G处,那么四边形BCFE的面积等于________.
如图,将边长为4的正方形ABCD沿着折痕EF折叠,使点B落在边AD的中点G处,那么四边形BCFE的面积等于________. 解:由题意,点C与点H,
解:由题意,点C与点H, ,tan∠1=
,tan∠1= .
. ,
,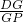 =
= ,
, ,
, ,
, ,
, .
. (FC+BE)×BC=
(FC+BE)×BC= ×(
×( +2.5)×4=6.
+2.5)×4=6.

 阅读快车系列答案
阅读快车系列答案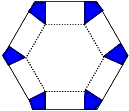 如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为
如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为
 (2013•丰南区一模)如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为
(2013•丰南区一模)如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为 (2012•惠城区模拟)如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长
(2012•惠城区模拟)如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长 如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )
如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )