
若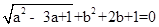 ,则
,则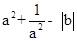 = .
= .
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源:2014届山东省泰安市泰山区初三下学期期末数学试卷(解析版) 题型:填空题
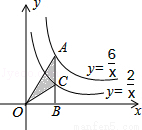
如图,点A是反比例函数y=的图象上﹣点,过点A作AB⊥x轴,垂足为点B,线段AB交反比例函数y=的图象于点C,则△OAC的面积为 _________ .
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学立体图形(解析版) 题型:填空题
如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为 m(容器厚度忽略不计).

查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学概率(解析版) 题型:选择题
如图所示为一个污水净化塔内部,污水从上方入口进入后流经形如等腰直角三角形的净化材枓表面,流向如图中箭头所示,每一次水流流经三角形两腰的机会相同,经过四层净化后流入底部的5个出口中的一个.下列判断:①5个出口的出水量相同;②2号出口的出水量与4号出口的出水量相同;③1,2,3号出水口的出水量之比约为1:4:6;④若净化材枓损耗的速度与流经其表面水的数量成正比,则更换最慢的一个三角形材枓使用的时间约为更换最快的一个三角形材枓使用时间的8倍.其中正确的判断有( )个.

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学整式(解析版) 题型:选择题
下列计算正确的是( )
A.a3+a2=a5 B.(3a﹣b)2=9a2﹣b2
C.(﹣ab3)2=a2b6 D.a6b÷a2=a3b
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学数的规律(解析版) 题型:填空题
一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即23=3+5;33=7+9+11;43=13+15+17+19;…;若63也按照此规律来进行“分裂”,则63“分裂”出的奇数中,最大的奇数是 .
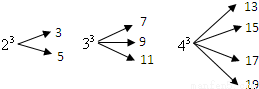
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学数形结合思想(解析版) 题型:选择题
数形结合是数学中常用的思想方法,试运用这一思想方法确定函数y=x2+1与y=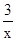 的交点的横坐标x0的取值范围是( )
的交点的横坐标x0的取值范围是( )
A.0<x0<1
B.1<x0<2
C.2<x0<3
D.﹣1<x0<0
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学圆(解析版) 题型:解答题
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤5).以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连接CD、QC.
(1)求当t为何值时,点Q与点D重合?
(2)设△QCD的面积为S,试求S与t之间的函数关系式,并求S的最大值;
(3)若⊙P与线段QC只有一个交点,请直接写出t的取值范围.

查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形的折叠(解析版) 题型:填空题
如图,在△ABC中,AB=AC,BC=8,tanC=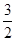 ,如果将△ABC沿直线l翻折后,点B落在边AC的中点处,直线l与边BC交于点D,那么BD的长为 .
,如果将△ABC沿直线l翻折后,点B落在边AC的中点处,直线l与边BC交于点D,那么BD的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com