
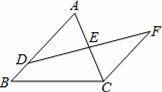
如图,D是△ABC的边AB上一点,E是AC的中点,过点C作CF∥AB,交DE的延长线于点F.求证:AB=CF+BD.

科目:初中数学 来源: 题型:
下列四个命题中,假命题是( )
A.两角对应相等,两个三角形相似
B.三边对应成比例,两个三角形相似
C.两边对应成比例且其中一边的对角相等,两个三角形相似
D.两边对应成比例且夹角相等,两个三角形相似
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,四边形ABCD是菱形,对角线AC与BD交于点O,且AC=80,BD=60.动点M、N分别以每秒1个单位的速度从点A、D同时出发,分别沿A→O→D和D→A运动,当点N到达点A时,M、N同时停止运动.设运动时间为t秒.
(1)求菱形ABCD的周长;
(2)记△DMN的面积为S,求S关于t的解析式,并求S的最大值;
(3)当t=30秒时,在线段OD的垂直平分线上是否存在点P,使得∠DPO=∠DON?若存在,这样的点P有几个?并求出点P到线段OD的距离;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
随着体育中考的临近,我校随机地调查了50名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:
| 时间(小时) | 5 | 6 | 7 | 8 |
| 人数 | 4 | 15 | 15 | 16 |
则这50名学生这一周在校的体育锻炼时间的众数为 ,平均数为
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,将平行四边形ABCD折叠,使顶点D恰落在AB边上的点M处,折痕为AN,那么对于结论 ①MN∥BC,②MN=AM,下列说法正确的是( )


A.①②都对 B.①②都错 C.①对②错 D.①错②对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com