
【题目】已知tan∠MON=2,矩形ABCD的边AB在射线OM上,AD=2,AB=m,CF⊥ON,垂足为点F.
(1)如图(1),作AE⊥ON,垂足为点E. 当m=2时,求线段EF的长度;
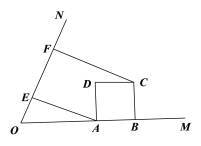
图(1)
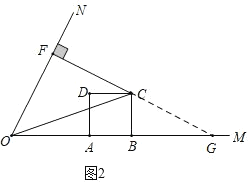
(2)如图(2),联结OC,当m=2,且CD平分∠FCO时,求∠COF的正弦值;
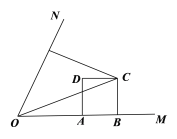
图(2)
(3)如图(3),当△AFD与△CDF相似时,求m的值.
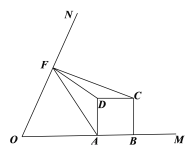
图(3)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)1或2或
;(3)1或2或![]() .
.
【解析】
(1)如图1,延长FC交OM于点G,证∠BCG=∠MON,在Rt△AOE中,设OE=a,可求得OA,OG,OF的长,则![]() ;
;
(2)如图2,延长FC交OM于点G,由(1)得![]() ,推出
,推出![]() ,在Rt△COB中,由勾股定理求出a的值,得出OF的长,可求出cos∠COF的值,进一步推出sin∠COF的值;
,在Rt△COB中,由勾股定理求出a的值,得出OF的长,可求出cos∠COF的值,进一步推出sin∠COF的值;
(3)需分情况讨论:当D在∠MON内部时,△FDA∽△FDC时,此时CD=AD=2,m=2;当△FDA∽△CDF时,延长CD交ON于点Q,过F作FP⊥CQ于P,可利用三角函数求出m的值;当D在∠MON外部时,可利用相似的性质等求出m的值.
解:解:(1)如图1,
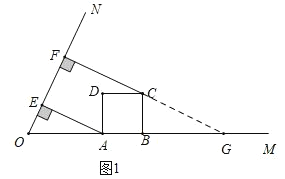
延长![]() 交
交![]() 于点
于点![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
则![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,
中,
设![]() ,由
,由![]() ,
,
可得![]() ,则
,则![]() ,
,![]() ,
,
![]() ;
;
(2)如图2,
延长![]() 交
交![]() 于点
于点![]() ,由(1)得
,由(1)得![]() ,
,
![]() 平分
平分![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,由
中,由![]() ,
,
得![]() ,
,
解得![]() (舍去),
(舍去),![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(3)当![]() 在
在![]() 内部时,
内部时,
①如图![]() ,
,
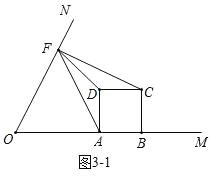
![]() 时,此时
时,此时![]() ,
,
![]() ;
;
②当![]() 时,
时,
如图![]() ,
,
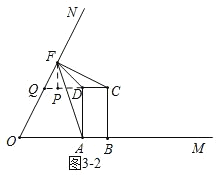
延长![]() 交
交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ;
;
当![]() 在
在![]() 外部时,
外部时,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
如图![]() ,
,
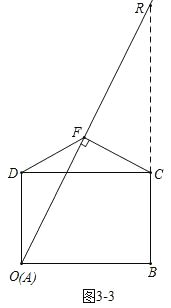
![]() 时,此时
时,此时![]() ,
,
![]() ,
,
![]() ,
,
![]() 、
、![]() 重合,
重合,
延长![]() 交
交![]() 于
于![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ;
;
如图![]() ,
,
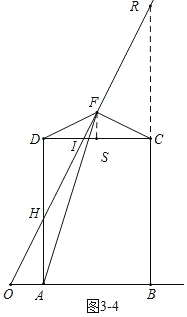
![]() 时,设
时,设![]() ,
,
延长![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
解得,![]() ,
,![]() (舍去),
(舍去),
![]() ,矛盾,
,矛盾,
综上所述:![]() 或
或![]() ,或
,或![]() .
.


科目:初中数学 来源: 题型:
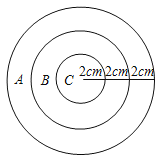
【题目】如图为一个封闭的圆形装置,整个装置内部为A、B、C三个区域(A、B两区域为圆环,C区域为小圆),具体数据如图.
(1)求出A、B、C三个区域三个区域的面积:SA= ,SB= ,SC= ;
(2)随机往装置内扔一粒豆子,多次重复试验,豆子落在B区域的概率PB为多少?
(3)随机往装置内扔180粒豆子,请问大约有多少粒豆子落在A区域?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
将一个多位自然数分解为个位与个位之前的数,让个位之前的数减去个位数的两倍,若所得之差能被7整除,则原多位自然数一定能被7整除.也称这个数为“要塞数”.例如:将数1078分解为8和107,107﹣8×2=91,因为91能被7整除,所以1078能被7整除,就称1078为“要塞数”.
完成下列问题:
(1)若一个三位自然数是“要塞数”,且个位数字和百位数字都是7,则这个三位自然数位 ;
(2)若一个四位自然数M是“要塞数”,设M的个位数字为x,十位数字为y,且个位数字与百位数字的和为13,十位数字与千位数字的和也为13,记F(M)=|x﹣y|,求F(M)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学要利用长为24m的篱笆围成一个长方形花圃,形状如图,一边靠墙(墙的最大可用长度为9m),中间隔有一道篱笆,设AB长为x米,围成的花圃面积为S平方米.
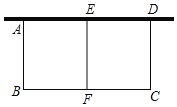
(1)求S关于x的函数解析式;并写出自变量x的取值范围.
(2)当AB多长时,围成的花圃有最大面积?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C.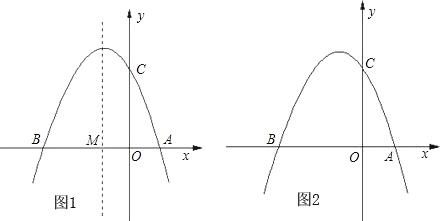
(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由;
(3)如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂设计了一款成本为20元件的工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价x(元件) | … | 30 | 40 | 50 | 60 | … |
每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
(1)研究发现,每天销售量y与单价x满足一次函数关系,求出y与x的关系式;
(2)当地物价部门规定,该工艺品销售单价最高不能超过50元件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润8000元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com