练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    已知抛物线y=ax2+bx+c与x轴的两个公共点之间的距离为1．若将抛物线y=ax2+bx+c向上平移一个单位，则它与x轴只有一个公共点；若将抛物线y=ax2+bx+c向下平移一个单位，则它经过原点，则抛物线y=ax2+bx+c为（　　）
    A、y=4x2+4
    		2
    x+1
    B、y=4x2+4
    		2
    x+1或y=4x2-4
    		2
    x+1
    C、y=4x2+4
    		2
    x-1
    D、y=4x2+4
    		2
    x-1或y=4x2-4
    		2
    x-1
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图所示，二次函数y=ax2+bx+c（a≠0）的图象经过点（-1，2），且与x轴交点的横坐标为x1、x2，其中-2＜x1＜-1、0＜x2＜1．下列结论：
    ①4a-2b+c＜0，②2a-b＜0，③a＜-1，④b2+8a＞4ac，⑤abc＜0，
    正确的结论是（　　）
    A、2个B、3个C、4个D、5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    把抛物线y=x2向下平移2个单位，再向右平移4个单位后得到的抛物线是（　　）
    A、y=（x+4）2+2B、y=（x-4）2+2C、y=（x+4）2-2D、y=（x-4）2-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    若二次函数y=x2-2x+c的图象与y轴的交点为（0，-3），则此二次函数有（　　）
    A、最小值为-2B、最小值为-3C、最小值为-4D、最大值为-4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    若关于x的一元二次方程x2+ax+b=0有两个不同的实数根m，n（m＜n），方程x2+ax+b=1有两个不同的实数p，q（p＜q），则m，n，p，q的大小关系为（　　）
    A、m＜p＜q＜nB、p＜m＜n＜qC、m＜p＜n＜qD、p＜m＜q＜n

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图是二次函数y=-x2+2x+4的图象，使y≤1成立的x的取值范围是（　　）
    A、-1≤x≤3B、x≤-1C、x≥1D、x≤-1或x≥3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

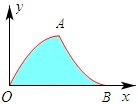    曲线y=
    -0.5(x-2)2+2，(0≤x≤2)
    0.5(x-4)2，(2≤x≤4)
    与x轴围成的面积（即图中阴影部分的面积）是多少？下面是课堂教学上同学们的看法，其中最佳答案是（　　）
    A、曲线不是圆弧，我们没有学过相关的方法，求不出来
    B、既然老师出了这道题，肯定是我们能求出来的，哪个神仙来做
    C、我们可以试一试，也许用面积分割的方法能求出来，我猜是4
    D、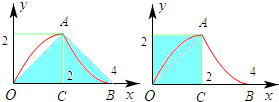
    我想出来了，是4；连接OA、OB，作AC⊥OB于C，OC=BC=AC=2，△OAB是等腰直角三角形，又因为分段的两部分对应的二次项系数的绝对值相等，所以这两段抛物线的形状相同，它们自变量的取值长度也相等，都是2，所以分割的部经过剪切，旋转，平移可以填补，就象图中这样，原来的阴影部分面积等于等腰Rt△OAB，也等于那个正方形的面积，是4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在研究相似问题时，甲、乙同学的观点如下：
    甲：将边长为3、4、5的三角形按图1的方式向外扩张，得到新三角形，它们的对应边间距为1，则新三角形与原三角形相似．
    乙：将邻边为3和5的矩形按图2的方式向外扩张，得到新的矩形，它们的对应边间距均为1，则新矩形与原矩形不相似．
    对于两人的观点，下列说法正确的是（　　）
    A、两人都对B、两人都不对C、甲对，乙不对D、甲不对，乙对

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，△ABC中，AE交BC于点D，∠C=∠E，AD：DE=3：5，AE=8，BD=4，则DC的长等于（　　）
    A、
    15
    4
    B、
    12
    5
    C、
    20
    3
    D、
    17
    4

    查看答案和解析>>

    同步练习册答案