
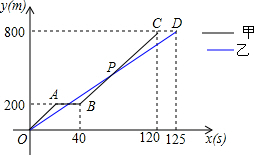
 在800米跑步测试过程中,甲乙两名运动员同时起跑,刚跑出200米时甲不慎摔倒,他又迅速爬起来再次投入比赛,并最终超越乙取得优异成绩.图中分别表示甲、乙两名运动员所跑的路程y(m)与比赛时间x(s)之间的关系.
在800米跑步测试过程中,甲乙两名运动员同时起跑,刚跑出200米时甲不慎摔倒,他又迅速爬起来再次投入比赛,并最终超越乙取得优异成绩.图中分别表示甲、乙两名运动员所跑的路程y(m)与比赛时间x(s)之间的关系.分析 (1)观察图象可知,(0-200)m之间,相对于y轴,甲的图象高于乙;
(2)分别求出线段OD和线段BC的解析式,联立解析式可得:$\frac{32}{5}x=\frac{15}{2}x-100$,解得:$x=\frac{1000}{11}$,再减去40即可解答.
解答 解:(1)观察图象可知,(0-200)m之间,相对于y轴,甲的图象高于乙,
所以乙跑的速度慢,
故答案为:乙.
(2)解:设线段OD的解析式为y=kx,
∵(125,800)经过y=kx的图象
∴将点D的坐标(125,800)代入y=kx得:125k=800,
解得:$k=\frac{32}{5}$,
∴OD的解析式为$y=\frac{32}{5}x$,
设线段BC的方程为y=kx+b,
∵(120,800),(40,200)经过y=kx+b的图象,
∴把(120,800),(40,200)代入y=kx+b得:$\left\{\begin{array}{l}{120k+b=800}\\{40k+b=200}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{15}{2}}\\{b=-100}\end{array}\right.$,
∴BC的解析式为:$y=\frac{15}{2}x-100$,
联立OD的解析式为$y=\frac{32}{5}x$,BC的解析式为:$y=\frac{15}{2}x-100$,
可得:$\frac{32}{5}x=\frac{15}{2}x-100$,
解得:$x=\frac{1000}{11}$,
∴$\frac{1000}{11}-40=\frac{560}{11}$(S)
∴甲再次投入比赛后,一共用了$\frac{560}{11}$秒才追上乙.
点评 本题考查了一次函数的应用,解决本题的关键是通过观察图象,从图象中找到所需要的信息,再利用已知点求出函数的解析式(待定系数法).


科目:初中数学 来源: 题型:选择题
| A. | m<x<n | B. | 2m<x<2n | C. | n-m<x<n+m | D. | 2n-2m<x<2n+2m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
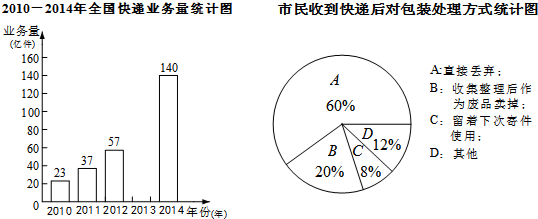
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
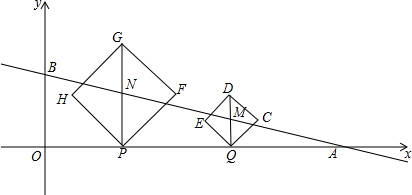
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
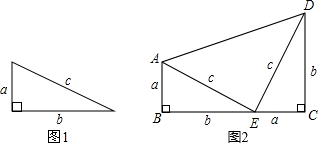
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com