
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣6,0),B(﹣1,1),C(﹣3,3),将△ABC绕点B顺时针方向旋转90°后得到△A1BC1 . 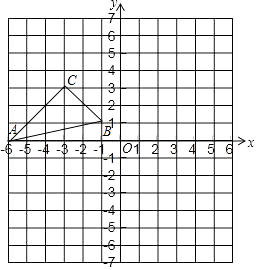
(1)画出△A1BC1 , 写出点A1、C1的坐标;
(2)计算线段BA扫过的面积.
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的南偏东60°方向,距离灯塔40海里的A处,它计划沿正北方向航行,去往位于灯塔P的北偏东45°方向上的B处.问B处距离灯塔P有多远?(结果精确到0.1海里) (参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732,
≈1.732, ![]() ≈2.449)
≈2.449)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论: ①4a+b=0;
②9a+c<3b;
③25a+5b+c=0;
④当x>2时,y随x的增大而减小.
其中正确的结论有( )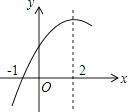
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,反比例函数y= ![]() (x>0)的图象经过点A(2
(x>0)的图象经过点A(2 ![]() ,1),射线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
,1),射线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D. 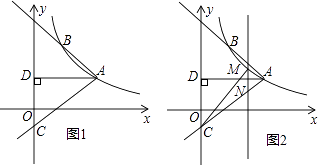
(1)求k的值;
(2)求tan∠DAC的值及直线AC的解析式;
(3)如图2, 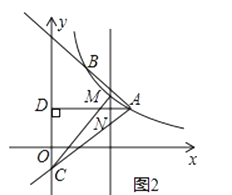
M是线段AC上方反比例函数图象上一动点,过M作直线l⊥x轴,与AC相交于点N,连接CM,求△CMN面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为( ![]() ,1),下列结论:①ac<0;②a+b=0;③4ac﹣b2=4a;④a+b+c<0.其中正确结论的个数是( )
,1),下列结论:①ac<0;②a+b=0;③4ac﹣b2=4a;④a+b+c<0.其中正确结论的个数是( ) 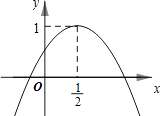
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AD平分∠BAC交⊙O于点D,过点D作DE∥BC交AC的延长线于点E. 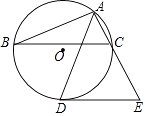
(1)试判断DE与⊙O的位置关系,并证明你的结论;
(2)若∠E=60°,⊙O的半径为5,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确的结论有(填序号). 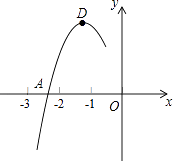
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4. 如图2,正方形ABCD顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.
如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D;若第二次掷得2,就从D开始顺时针连续跳2个边长,落到圈B;…
设游戏者从圈A起跳.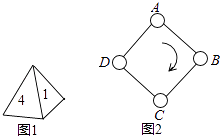
(1)嘉嘉随机掷一次骰子,求落回到圈A的概率P1;
(2)淇淇随机掷两次骰子,用列表法求最后落回到圈A的概率P2 , 并指出她与嘉嘉落回到圈A的可能性一样吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把边长相等的正五边形ABGHI和正六边形ABCDEF的AB边重合,按照如图的方式叠合在一起,连接EB,交HI于点K,则∠BKI的大小为( ) 
A.90°
B.84°
C.72°
D.88°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com