练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．直角三角形斜边长是5，一直角边的长是3，则此直角三角形的面积为6．

    分析 根据直角三角形的斜边与一条直角边，可利用勾股定理求出另一条直角边的长度，再根据三角形的面积公式求出面积即可．

    解答 解：∵直角三角形斜边长是5，一直角边的长是3，
    ∴另一直角边长为$\sqrt{{5}^{2}-{3}^{2}}$=4．
    该直角三角形的面积S=$\frac{1}{2}$×3×4=6．
    故答案为：6．

    点评 本题考查了勾股定理以及三角形的面积公式，解题的关键是根据勾股定理求出另一条直角边的长度．本题属于基础题，难度不大，解决该题型题目时，根据勾股定理找出直角三角形的三边关系是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    8．下列命题中，属于真命题的是（　　）
    A．同位角互补
    B．多边形的外角和小于内角和
    C．平方根等于本身的数是1
    D．同一平面内，垂直于同一条直线的两条直线平行

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

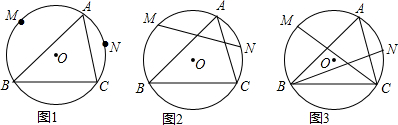
    9．中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽，他为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”（如图1）．图2由弦图变化得到，它是用八个全等的直角三角形拼接而成．将图中正方形MNKT，正方形EFGH，正方形ABCD的面积分别记为S1，S2，S3，若S1+S2+S3=18，则正方形EFGH的面积为（　　）
    A．9B．6C．5D．$\frac{9}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．计算：$\frac{2a}{{{a^2}-16}}-\frac{1}{a-4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．已知分式$\frac{{m}^{2}-9}{m+3}$的值是0，则m的值为3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．下面哪个点在函数y=$\frac{1}{2}$x+1的图象上（　　）
    A．（-2，0）B．（-2，1）C．（2，0）D．（2，1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

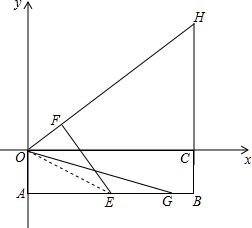    4．如图，矩形OABC中，OA在y轴的负半轴上，OC在x轴的正半轴上，OA=1，OC=4，E是AB的中点，将矩形沿OE折叠，点A与点F重合，延长OF、BC交于点H，G是射线AB上一点，将△OAG绕点O旋转，使得点A落在OE上，记旋转后的三角形为△OA′G′，A′G′与OH交于点M，若∠MHG′=∠MHB，则AG的长为$\frac{2+20\sqrt{5}}{11}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．已知一个直角三角形的两条直角边的差为2，两条直角边的平方和为8，则这个直角三角形的面积是1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图1，⊙O是△ABC的外接圆，已知：AB≠AC，点M是$\widehat{AB}$的中点，点N是$\widehat{AC}$的中点，按要求解答下列问题：
    （1）如图2，连接MN交AB于点E，交AC于点F．
    ①求证：AE=AF；②若2ME•NF=EF2，求∠A的度数；
    （2）如图3，连接CM，BN，若CM=BN，求∠A的度数．
    （3）在图1中，①仅用直尺找出点P，使点P为$\widehat{BC}$的中点；②连出六边形AMBPCN，已知⊙O的半径为1，△ABC的周长为4，求六边形AMBPCN的面积．

    查看答案和解析>>

    同步练习册答案