
| A��ˮ��/�� | B��ˮ��/�� | |
| �� | 11Ԫ | 17Ԫ |
| �ҵ� | 9Ԫ | 13Ԫ |
���� ��1��������������ӯ�����ɣ�
��2����A��ˮ������x�䣬B��ˮ������y�䣬�г���ϵʽ���ҳ�x��y�ķǸ������⣬��дһ��������ɣ�
��3�������A��ˮ��x�䣬�ֱ��ʾ������ҵ��Aˮ����Bˮ��������������ӯ����С��115Ԫ���в���ʽ��⣮
��� �⣺��1��������ӯ��Ϊ��5��11+5��9+5��17+5��13=250��Ԫ����
��2����A��ˮ������x�䣬B��ˮ������y�䣬����ҵ�ֱ��ǣ�10-x���䣬��10-y���䣬��������ã�11x+17y=9��10-x��+13��10-y����
��2x+3y=22��
��Ǹ��������ǣ�$\left\{\begin{array}{l}{x=2}\\{y=6}\end{array}\right.$��$\left\{\begin{array}{l}{x=5}\\{y=4}\end{array}\right.$��$\left\{\begin{array}{l}{x=8}\\{y=2}\end{array}\right.$��
���һ�������2��8��6��4���ڶ��������5��5��4��6�������������8��2��2��8��
����һ��������㣺��2��11+17��6����2=248��Ԫ����
���ڶ���������㣺��5��11+4��17����2=246��Ԫ����
��������������㣺��8��11+2��17����2=244��Ԫ����
�ʴ��ǣ�2��8��6��4��
��3�������A��ˮ��x�䣬�����B��ˮ����10-x���䣬
�ҵ���A��ˮ����10-x���䣬�ҵ���B��ˮ��10-��10-x��=x�䣬
��9����10-x��+13x��115��
��ã�x��6.25��
�֡�x��10��xΪ������
��x=7��8��9��10��
�������֪��x=7ʱӯ�����ӯ��Ϊ��246Ԫ��
��ʱ����Ϊ������A��ˮ��7�䣬B��ˮ��3�䣬�ҵ���A��ˮ��3�䣬B��ˮ��7�䣬���ӯ��Ϊ246Ԫ��
���� ���⿼����һԪһ�β���ʽ���Ӧ�ã�Ū�����⣬������Ŀ�IJ�ͬҪ�������ѽ����Ŀ�����⣬ѧ����һ�κ�������ʽ���Ա���ȡֵ��Χ�������ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
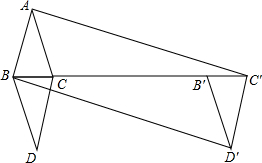 ��ͼ����ABC�У�AB=AC=3��BC=2������ABC��BC���ۣ��á�DBC���ٽ���DBC������BC����ƽ��k�������������D��B��C�䣬���ı���ABD��C���Ǿ��Σ���k=7��
��ͼ����ABC�У�AB=AC=3��BC=2������ABC��BC���ۣ��á�DBC���ٽ���DBC������BC����ƽ��k�������������D��B��C�䣬���ı���ABD��C���Ǿ��Σ���k=7���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4a2+2ab+b2 | B�� | m2+2mn+n2 | C�� | m2n2-mn+1 | D�� | 4x2+10x+25 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC��AC=BC����C=90�㣬CD=1��AD�ǡ�ABC�Ľ�ƽ���ߣ�DE��AB���ڵ�E����AC�ij�Ϊ$\sqrt{2}$+1��
��ͼ���ڡ�ABC��AC=BC����C=90�㣬CD=1��AD�ǡ�ABC�Ľ�ƽ���ߣ�DE��AB���ڵ�E����AC�ij�Ϊ$\sqrt{2}$+1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com