
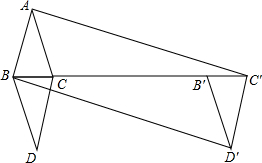
 如图,△ABC中,AB=AC=3,BC=2,将△ABC沿BC翻折,得△DBC,再将△DBC沿射线BC方向平移k个距离得三角形D′B′C′,若四边形ABD′C′是矩形,则k=7.
如图,△ABC中,AB=AC=3,BC=2,将△ABC沿BC翻折,得△DBC,再将△DBC沿射线BC方向平移k个距离得三角形D′B′C′,若四边形ABD′C′是矩形,则k=7. 分析 过点D′作D′E⊥B′C′,垂足为E.首先求得EC′=1,然后证明△BAC′∽△C′ED′,从而可求得BC′=9,最后根据CC′=BC′-BC可求得平移的距离即k的值.
解答 解:如图所示:过点D′作D′E⊥B′C′,垂足为E.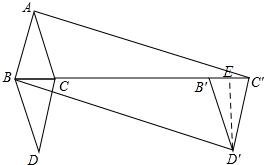
由翻折和平移的性质可知:B′D′=B′C′=3,B′C′=2,
∵B′D′=B′C′,D′E⊥B′C′,
∴EC′=$\frac{1}{2}B′C′$=1.
∵四边形ABD′C′是矩形,
∴∠AC′B+∠BC′D′=90°.
又∵∠BC′D+∠ED′C′=90°,
∴∠ED′C′=∠AC′B.
又∵∠BAC′=∠C′ED′,
∴△BAC′∽△C′ED′.
∴$\frac{AB}{BC′}=\frac{EC′}{C′D′}$即$\frac{3}{BC′}=\frac{1}{3}$.
∴BC′=9.
∴CC′=BC′-BC=9-2=7.
∴k=7.
故答案为:7.
点评 本题主要考查的是相似三角形的性质和判定、矩形的性质、等腰三角形的性质、翻折变换、平移变换,证得△BAC′∽△C′ED′是解题的关键.


科目:初中数学 来源: 题型:解答题
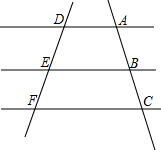 如图,已知AD∥EB∥FC,你能得到以下结论吗?说明理由.
如图,已知AD∥EB∥FC,你能得到以下结论吗?说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
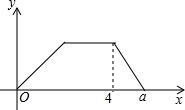 最近重庆八中学生宿舍在增修安全通道,一辆拉砖的货车从仓库匀速驶往学校,到达后用了1小时卸货,随即匀速返回.已知货车返回的速度是它从仓库驶往学饺的速度的2倍,货车离仓库的距离y(千米)关于时间x的函数图象如图所示.则a=4.5(小时).
最近重庆八中学生宿舍在增修安全通道,一辆拉砖的货车从仓库匀速驶往学校,到达后用了1小时卸货,随即匀速返回.已知货车返回的速度是它从仓库驶往学饺的速度的2倍,货车离仓库的距离y(千米)关于时间x的函数图象如图所示.则a=4.5(小时).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
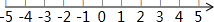
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
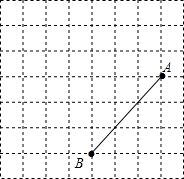 请在网格中建立平面直角坐标系,使得A点的坐标为(4,2).
请在网格中建立平面直角坐标系,使得A点的坐标为(4,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A种水果/箱 | B种水果/箱 | |
| 甲店 | 11元 | 17元 |
| 乙店 | 9元 | 13元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com