
【题目】如果一个角的两边与另一个角的两边分别平行,某同学为了探究这两个角的关系,画出来以下两个不同的图形,请你根据图形完成以下问题:
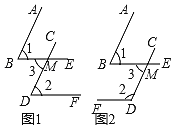
(1)如图1,如果AB∥CD,BE∥DF,那么∠1与∠2的关系是 ;
如图2,如果AB∥CD,BE∥DF,那么∠1与∠2的关系是 ;
(2)根据(1)的探究过程,我们可以得到结论:如果一个角的两边与另一个角的两边分别平行,那么这两个角的关系是 ;
(3)利用结论解决问题:如果有两个角的两边分别平行,且一个角比另一个角的3倍少40°,则这两个角分别是多少度?
【答案】(1)相等,互补;(2)相等或互补;(3)20°,20°或55°,125°.
【解析】
(1)根据平行线的性质推出即可;
(2)根据(1)的结论得出即可;
(3)先得出方程,再求出方程的解即可.
解:(1)∵AB∥CD,BE∥DF,
∴∠1=∠3,∠2=∠3,
∴∠1=∠2,
即∠1与∠2的关系是相等,
图2中∵AB∥CD,BE∥DF,
∴∠1=∠3,∠2+∠3=180°,
∴∠1+∠2=180°,
即∠1与∠2的关系是互补,
故答案为:相等,互补;
(2)如果一个角的两边与另一个角的两边分别平行,那么这两个角的关系是相等或互补,故答案为:相等或互补;
(3)设两个角为x°和2x°﹣40°,
∵有两个角的两边分别平行,且一个角比另一个角的3倍少40°,
∴x=3x﹣40或x+3x﹣40=180,
解得:x=20或x=55,
即这两个角为20°,20°或55°,125°.


科目:初中数学 来源: 题型:
【题目】茜茜受《乌鸦喝水》故事的启发,利用量筒、大球和小球进行了如下操作,请根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高______cm,放入一个大球水面升高______cm.
(2)如果要使水面上升到50cm,应放入大球、小球各多少个?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分) 小丽想用一块面积为400cm2的正方形纸片,沿着边的方向裁处一块面积为300cm2的长方形纸片.(1)请帮小丽设计一种可行的裁剪方案;
(2)若使长方形的长宽之比为3:2,小丽能用这块纸片裁处符合要求的纸片吗?若能,请帮小丽设计一种裁剪方案,若不能,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分) 如图1,将△ABC纸片沿中位线EH折叠,使点A的对称点D落在BC边上,再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF,HG折叠,折叠后的三个三角形拼合形成一个矩形.类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩 形,这样的矩形称为叠合矩形.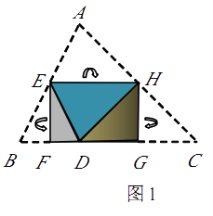
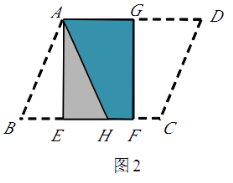

(1)将□ABCD纸片按图2的方式折叠成一个叠合矩形AEFG,则操作形成的折痕分别是线段 , ;S矩形AEFG:S□ABCD=
(2)ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH,若EF=5,EH=12,求AD的长.
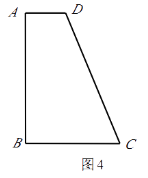
(3)如图4,四边形ABCD纸片满足AD∥BC,AD<BC,AB⊥BC,AB=8,CD=10.小明把该纸片折叠,得到叠合正方形.请你帮助画出叠合正方形的示意图,并求出AD,BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对代数式![]() ,老师要求任意取一个x的值后求出代数式的值.圆圆发现,大家所求得的代数式的值都大于等于0,即x=-3时代数式的最小值是0.利用这个发现,圆圆试着写出另外一些结论:①在x=-3时,代数式(x+3)2+2的最小值为2;②在a=-b时,代数式(a+b)2+m的最小值为m;③在c=-d时,代数式-(c+d)2+n的最大值为n;④在
,老师要求任意取一个x的值后求出代数式的值.圆圆发现,大家所求得的代数式的值都大于等于0,即x=-3时代数式的最小值是0.利用这个发现,圆圆试着写出另外一些结论:①在x=-3时,代数式(x+3)2+2的最小值为2;②在a=-b时,代数式(a+b)2+m的最小值为m;③在c=-d时,代数式-(c+d)2+n的最大值为n;④在![]() 时,代数式
时,代数式![]() 的最大值为29.其中正确的为( )
的最大值为29.其中正确的为( )
A. ①②③B. ①③C. ①④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数 ![]() 的图象与一次函数
的图象与一次函数 ![]() 的图象交于点A(1,4)、点B(-4,n).
的图象交于点A(1,4)、点B(-4,n).
(1)求 ![]() 和
和 ![]() 的值;
的值;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(阅读理解)
如图(1),AD是△ABC的中线,作△ABC的高AH.
∵AD是△ABC的中线
∴BD=CD
∵S△ABD=![]() BDAH,S△ACD=
BDAH,S△ACD=![]() CDAH
CDAH
∴S△ABD S△ACD(填:<或>或=)
(2)(结论拓展)
△ABC中,D是BC边上一点,若![]() ,则
,则![]() =
=
(3)(结论应用)
如图(3),请你将△ABC分成4个面积相等的三角形(画出分割线即可)
如图(4),BE是△ABC的中线,F是AB边上一点,连接CF交BE于点O,若![]() ,则
,则![]() = .说明你的理由
= .说明你的理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知一个多边形的内角和是它的外角和的 3 倍,求这个多边形的边数.
(2)如图,点F 是△ABC 的边 BC 延长线上一点.DF⊥AB,∠A=30°,∠F=40°,求∠ACF 的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com