
(本题满分10分)如图所示,菱形 的顶点
的顶点 、
、 在
在 轴上,点
轴上,点 在点
在点
的左侧,点 在
在 轴的正半轴上,
轴的正半轴上, ,点
,点 的坐标为(-2,0).
的坐标为(-2,0).

(1)求 点的坐标;
点的坐标;
(2)求直线 的函数关系式;
的函数关系式;
(3)动点 从点
从点 出发,以每秒1个单位长度的速度,按照
出发,以每秒1个单位长度的速度,按照 →
→ →
→ →
→ →
→ 的顺序在菱形的边上匀速运动一周,设运动时间为
的顺序在菱形的边上匀速运动一周,设运动时间为 秒.求
秒.求 为何值时,以点
为何值时,以点 为圆心、以1为半径的圆与对角线
为圆心、以1为半径的圆与对角线 相切?
相切?
(1) ;(2)
;(2)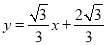 ;(3)
;(3) 或
或 或
或 或
或
【解析】
试题分析:(1)根据菱形的性质和等边三角形的性质求得即可;(2)求直线解析式的基本方法是待定系数法,在(1)中已求得 坐标的基础上,将
坐标的基础上,将 、
、 坐标代入设好的直线解析式,求出系数即可;(3)本小题可先结合图作一大胆猜想,再根据切线定义和含
坐标代入设好的直线解析式,求出系数即可;(3)本小题可先结合图作一大胆猜想,再根据切线定义和含 的直角三角形的性质,将时间问题转换为距离问题,注意分类讨论要讨论完全.
的直角三角形的性质,将时间问题转换为距离问题,注意分类讨论要讨论完全.
试题解析:(1) 菱形
菱形 中,点
中,点 的坐标为
的坐标为 ,
, ,
,
 为正三角形
为正三角形  ,
,




(2)由(1)得  设直线
设直线 的函数表达式为
的函数表达式为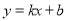 ,则
,则
 解得
解得
 直线
直线 的函数表达式为
的函数表达式为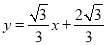
(3)由图可猜想,有四个满足要求的圆  四边形
四边形 是菱形
是菱形  ,
, ,
,
如图所示,

①点 在
在 上与
上与 相切时,
相切时,

②点 在
在 上与
上与 相切时,
相切时,



③点 在
在 上与
上与 相切时,
相切时,


④点 在
在 上与
上与 相切时,
相切时,


综上,当 或
或 或
或 或
或 时,以点
时,以点 为圆心、以
为圆心、以 为半径的圆与对角线
为半径的圆与对角线 相切.
相切.
考点:1.菱形的性质;2.待定系数法求直线解析式;2.圆的切线的性质.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014-2015学年江西省吉安市朝宗实验学校九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,四边形OABC是矩形,ADEF是正方形,点A、D在 轴的正半轴上,点C在
轴的正半轴上,点C在 轴的正半轴上,点F在AB上,点B、E在反比例函数
轴的正半轴上,点F在AB上,点B、E在反比例函数 的图象上,OA=1,OC=6,则正方形ADEF的边长为_________.
的图象上,OA=1,OC=6,则正方形ADEF的边长为_________.
 、
、
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏盐城东台苏东双语学校九年级上学期第一次检测二数学试卷(解析版) 题型:计算题
(本题满分12分)如图,在边长为3的正方形ABCD中,点E是BC边上的点,BE=1,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F,

(1)求 的值为 .
的值为 .
(2)求证:AE=EP;
(3)在AB边上是否存在点M,使得四边形DMEP是平行四边形?若存在,请给予证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏盐城东台苏东双语学校九年级上学期第一次检测二数学试卷(解析版) 题型:填空题
一弦分圆周成两部分,其中一部分是另一部分的4倍,则这弦所对的圆周角度数为 ;
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏盐城东台苏东双语学校九年级上学期第一次检测二数学试卷(解析版) 题型:选择题
方程2x2-7=-3x 化成一般形式后,二次项系数、一次项系数、常数项分别是 ( )
(A)2,-7,-3 (B)2,-7,3 (C)2,3,-7 (D)2,3,7
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市锡山区九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分8分)如图,在 中,
中, ,
, 平分
平分 交
交 于点
于点 ,点
,点 在
在 边上且
边上且 .
.

(1)判断直线 与
与 外接圆的位置关系,并说明理由;
外接圆的位置关系,并说明理由;
(2)若 ,
, ,求
,求 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省孝感市孝南区三校九年级12月月考数学试卷(解析版) 题型:解答题
小明在解一元二次方程时,发现有这样一种解法:
如:解方程 .
.
【解析】
原方程可变形,得
 .
.
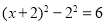 ,
,
 ,
,
 .
.
直接开平方并整理,得 .
.
我们称小明这种解法为“平均数法”.
(1)下面是小明用“平均数法”解方程 时写的解题过程.
时写的解题过程.
【解析】
原方程可变形,得
 .
.
 ,
,
 .
.
直接开平方并整理,得 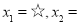 ¤.
¤.
上述过程中的“ ”,“
”,“ ” ,“☆”,“¤”表示的数分别为_____,_____,_____,_____.
” ,“☆”,“¤”表示的数分别为_____,_____,_____,_____.
(2)请用“平均数法”解方程: .
.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省陆丰市九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,在正方形ABCD中,F为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连结EF,若∠BEC=60°,那么∠EFD的度数为( )

A.10° B.15° C.20° D.25°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com