
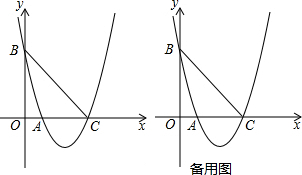
分析 (1)把A点、B点坐标分别代入二次函数y=$\frac{2}{3}$x2+bx+c,根据待定系数法即可求这个二次函数的表达式,进一步得到其图象的顶点坐标;
(2)如图,作点A关于直线BC的对称点A′,连AA′,交BC于F,过点A′作A′G⊥AC,交AC于G,由△ACF∽△BOC,求得AF,AA′,由△AA′G∽△BCO,求得AG,GA′,可得点A′的坐标;
(3)以AC为边作等边三角形ACT,以T为圆心,作经过A、C两点的辅助圆,圆T与y轴的交点即为所求,根据圆周角定理即可求解.
解答 解:(1)把A点、B点坐标分别代入二次函数y=$\frac{2}{3}$x2+bx+c,可得
$\left\{\begin{array}{l}{\frac{2}{3}×{2}^{2}+2b+c=0}\\{c=8}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-\frac{16}{3}}\\{c=8}\end{array}\right.$.
故这个二次函数的表达式${y_{\;}}=\frac{2}{3}{x^2}-\frac{16}{3}x+8$,顶点坐标为(4,-$\frac{8}{3}$);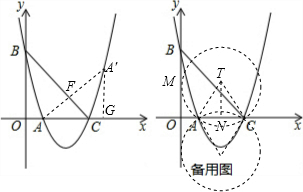 (2)求得C点的坐标(6,0),
(2)求得C点的坐标(6,0),
如图,作点A关于直线BC的对称点A′,连AA′,交BC于F,过点A′作A′G⊥AC,交AC于G,
AC=OC-OA=6-2=4,
BC=$\sqrt{O{C}^{2}+O{C}^{2}}$=10,
由△ACF∽△BCO,则$\frac{AF}{AC}$=$\frac{BO}{BC}$,即$\frac{AF}{4}$=$\frac{8}{10}$,解得AF=$\frac{16}{5}$,
∵点A关于直线BC的对称点A′,
∴AA′=$\frac{32}{5}$,
由△AA′G∽△BCO,
则$\frac{AA′}{AG}$=$\frac{BC}{BO}$,即$\frac{\frac{32}{5}}{AG}$=$\frac{10}{8}$,解得AG=$\frac{128}{25}$,
则$\frac{AA′}{GA′}$=$\frac{BC}{OC}$,即$\frac{\frac{32}{5}}{GA′}$=$\frac{10}{6}$,解得GA′=$\frac{96}{25}$,
故点A′的坐标为($\frac{178}{25}$,$\frac{96}{25}$);
(3)M(0,2$\sqrt{3}$)或M(0,-2$\sqrt{3}$).
如备用图,以AC为边作等边三角形ACT,以T为圆心,作经过A、C两点的辅助圆,圆T与y轴的交点即为所求.过T点作TN⊥AC于N,
∵AC=4,OA=2,三角形ACT是等边三角形,
∴ON=2+4÷2=4,TN=2$\sqrt{3}$,
∴M(0,2$\sqrt{3}$)或M(0,-2$\sqrt{3}$).
点评 本题考查了二次函数综合题,涉及待定系数法求二次函数解析式、顶点坐标的求法、相似三角形的性质、圆周角定理、探究等边三角形的性质等重要知识点,综合性强,能力要求极高.考查学生分类讨论,数形结合的数学思想方法.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
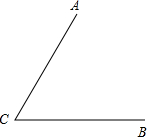 如图两条公路CA与CB,B,C是两个村庄,现在要建一个菜场,使它到两个村庄的距离相等而且还要使它到两条公路的距离也相等,用尺规作图画出菜场的位置(不写作法)保留作图痕迹.
如图两条公路CA与CB,B,C是两个村庄,现在要建一个菜场,使它到两个村庄的距离相等而且还要使它到两条公路的距离也相等,用尺规作图画出菜场的位置(不写作法)保留作图痕迹.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{8}{5}$ | B. | $\frac{3}{8}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com