
【题目】如图,已知∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=6,AC=3,则BE=( )
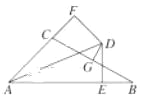
A. 6 B. 3 C. 2 D. 1.5
【答案】D
【解析】
首先连接CD,BD,由∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,根据角平分线的性质与线段垂直平分线的性质,易得CD=BD,DF=DE,继而可得AF=AE,易证得Rt△CDF≌Rt△BDE,则可得BE=CF,继而求得答案.
解:连接CD,BD,
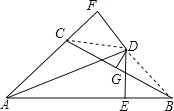
∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DF=DE,∠F=∠DEB=90°,∠ADF=∠ADE,
∴AE=AF,
∵DG是BC的垂直平分线,
∴CD=BD,
在Rt△CDF和Rt△BDE中,
![]() ,
,
∴Rt△CDF≌Rt△BDE(HL),
∴BE=CF,
∴AB=AE+BE=AF+BE=AC+CF+BE=AC+2BE,
∵AB=6,AC=3,
∴BE=1.5.
故选:D.


科目:初中数学 来源: 题型:
【题目】用同样大小的灰、白两种正方形地砖铺设地面,方法是(如图):第一层只有2块白色地砖,第二层是在第一层外面围一圈灰色地砖,第三层是在第二层外面围一圈白色地砖……
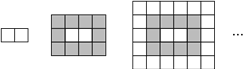
(1)第七层共有几块地砖,是白色的还是灰色的?
(2)第n层共有几块地砖(结果化成最简)?如果这些地砖是白色的,那么正整数n有什么特点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人,行驶路程记录如下(规定向南为正,向北为负,单位:km):

①接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
②若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
③若该出租车的计价标准为:行驶路程不超过3km收费10元,超过3km的部分按每千米加1.8元收费,在这过程中该驾驶员共收到车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在实践中学习:
(1)如图1所示:已知AB∥CD,∠ABD=115°,根据 可得出:∠BDC的度数是 .
(2)如图2所示:已知AB∥CD,∠ABC=25°,∠EDC=40°,求∠BED的度数.
(3)如图3所示:已知MA∥NC,试确定∠A、∠B、∠C和∠E、∠F的关系,并说明理由.
(4)如图4所示:已知AB∥CD,∠ABE=α,∠FCD=β,∠CFE=γ,且BE⊥EF,试确定α、β、γ的关系,请说明理由.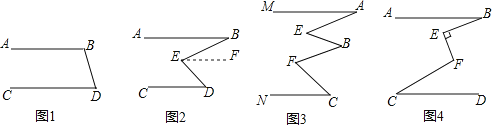
查看答案和解析>>
科目:初中数学 来源: 题型:
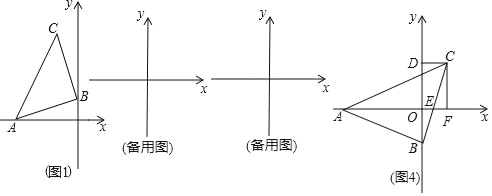
【题目】如图,△ABC为等腰直角三角形,∠ABC=90°,AB=BC,点A在x轴的负半轴上,点B是y轴上的一个动点,点C在点B的上方,
(1)如图1当点A的坐标为(﹣3,0),点B的坐标为(0,1)时,求点C的坐标;
(2)设点A的坐标为(a,0),点B的坐标为(0,b).过点C作CD⊥y轴于点D,在点B运动过程中(不包含△ABC的一边与坐标轴重合的情况),猜想线段OD的长与a、b的数量关系,并说明理由;
(3)在(2)的条件下如图4,当x轴平分∠BAC时,BC交x轴于点E,过点作CF⊥x轴于点F.说明此时线段CF与AE的数量关系(用含a、b的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOC=∠BOC,点P在OC上,PD⊥OA于点D,PE⊥OB于点E.若OD=8,OP=10,则PE的长为( ) 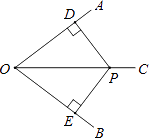
A.5
B.6
C.7
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=128°,∠C=36°,则∠DAE的度数是( ) 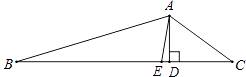
A.10°
B.12°
C.15°
D.18°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某银行去年新增加居民存款10亿元人民币.
(1)经测量,100张面值为100元的新版人民币大约厚0.9厘米,如果将10亿元面值为100元的新版人民币摞起来,大约有多高?
(2)一台激光点钞机的点钞速度是8×104张/时,按每天点钞5小时计算,如果让点钞机点一遍10亿元面值为100元的新版人民币,点钞机大约要点多少天?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)2﹣(﹣7)﹣13+(﹣7)
(2)18﹣6÷(﹣2)×(﹣![]() )
)
(3)﹣23÷[(﹣2)3﹣(﹣4)]
(4)(0.25﹣![]() ﹣
﹣![]() )×(﹣36)
)×(﹣36)
(5)0﹣23÷(﹣4)3﹣![]()
(6)﹣32×(﹣2)+42÷(﹣2)3﹣|﹣22|;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com