
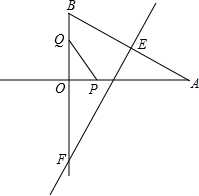
 如图,在Rt△AOB中,∠AOB=90°,AO=$\sqrt{3}$,BO=1,AB的垂直平分线交AB于点E,交射线BO于点F.点P从点A出发沿射线AO以每秒2$\sqrt{3}$个单位的速度运动,同时点Q从点O出发沿OB方向以每秒1个单位的速度运动,当点Q到达点B时,点P、Q同时停止运动.设运动的时间为t秒.
如图,在Rt△AOB中,∠AOB=90°,AO=$\sqrt{3}$,BO=1,AB的垂直平分线交AB于点E,交射线BO于点F.点P从点A出发沿射线AO以每秒2$\sqrt{3}$个单位的速度运动,同时点Q从点O出发沿OB方向以每秒1个单位的速度运动,当点Q到达点B时,点P、Q同时停止运动.设运动的时间为t秒.分析 (1)利用平行线的性质结合相似三角形的判定与性质得出△AEN∽△QOP,进而利用锐角三角函数关系求出即可;
(2)利用线段垂直平分线的性质得出△FBA是等边三角形,进而得出线段P′Q′与线段EF有公共点时t的最大值,进而得出答案.
解答 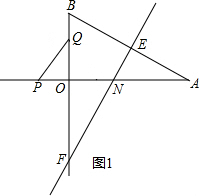 解:(1)如图1,当PQ∥EF时,
解:(1)如图1,当PQ∥EF时,
则∠QPO=∠ENA,
又∵∠AEN=∠QOP=90°,
∴△AEN∽△QOP,
∵∠AOB=90°,AO=$\sqrt{3}$,BO=1,
∴tanA=$\frac{BO}{AO}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠A=∠PQO=30°,
∴$\frac{PO}{QO}$=$\frac{\sqrt{3}}{3}$=$\frac{2\sqrt{3}t-\sqrt{3}}{t}$,
解得:t=$\frac{3}{5}$,
故当t=$\frac{3}{5}$时,PQ∥EF;
故答案为:$\frac{3}{5}$;
(2)如图2,当P点介于P1和P2之间的区域时,P1′点介于P1′和P2′之间,此时线段P′Q′与线段EF有交点,
当P运动到P1时,
∵AE=$\frac{1}{2}$AB=1,且易知△AEP1′∽△AOB,
∴$\frac{AE}{AO}=\frac{A{{P}_{1}}^{′}}{AB}$,∴AP1′=$\frac{2\sqrt{3}}{3}$,
∴P1O=P1′O=$\frac{\sqrt{3}}{3}$,
∴AP1=AO+P1O=$\frac{4\sqrt{3}}{3}$,
∴此时P点运动的时间t=$\frac{\frac{4\sqrt{3}}{3}}{2\sqrt{3}}$=$\frac{2}{3}$s,
当P点运动到P2时,
∵∠BAO=30°,∠BOA=90°,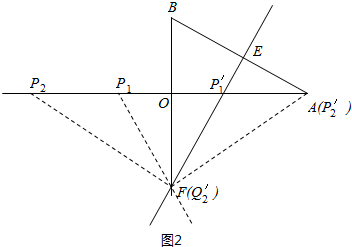
∴∠B=60°,
∵AB的垂直平分线交AB于点E,
∴FB=FA,
∴△FBA是等边三角形,
∴当PO=OA=$\sqrt{3}$时,此时Q2′与F重合,A与P2′重合,
∴PA=2$\sqrt{3}$,则t=1秒时,线段P′Q′与线段EF有公共点,
故当t的取值范围是:$\frac{2}{3}$≤t≤1.
故答案为:$\frac{2}{3}$≤t≤1.
点评 此题主要考查了相似三角形的判定与性质以及线段垂直平分线的性质、锐角三角三角函数关系等知识,得出临界点时t的最值是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{5x-3y=16}\\{3x-5y=0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=5}\\{2x-y=1}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{3x-y=1}\\{y=2x}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-y=2}\\{2x-2y=-4}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\overline{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x+y=180\\ y=x•25%\end{array}\right.$ | B. | $\left\{\begin{array}{l}x+y=180\\ x=y•25%\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x+y=180\\ x-y=25%\end{array}\right.$ | D. | $\left\{\begin{array}{l}x+y=180\\ y-x=25%\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com