
【题目】如图, ![]() 中,
中, ![]() ,
,![]() ,则
,则![]() 的度数为( )
的度数为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
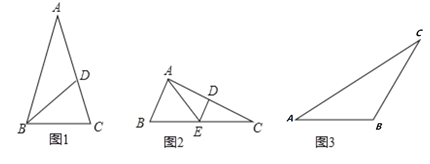
【题目】如果一个三角形能被一条线段割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形.
(1)如图1,![]() 是等腰锐角三角形,
是等腰锐角三角形,![]() ,若
,若![]() 的角平分线
的角平分线![]() 交
交![]() 于点
于点![]() ,且
,且![]() 是
是![]() 的一条特异线,则
的一条特异线,则![]() 度.
度.
(2)如图2,![]() 中,
中,![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() 是
是![]() 的一条特异线;
的一条特异线;
(3)如图3,若![]() 是特异三角形,
是特异三角形,![]() ,
,![]() 为钝角,不写过程,直接写出所有可能的
为钝角,不写过程,直接写出所有可能的![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月23日是世界读书日,在世界读书日来临之际,某校为了营造读书好、好读书、读好书的氛围,决定采购《童年》《汤姆![]() 索亚历险记》两种图书供学生阅读.通过了解,购买
索亚历险记》两种图书供学生阅读.通过了解,购买![]() 本《童年》、
本《童年》、![]() 本《汤姆
本《汤姆![]() 索亚历险记》共需
索亚历险记》共需![]() 元,购买
元,购买![]() 本《童年》、
本《童年》、![]() 本《汤姆
本《汤姆![]() 索亚历险记》共需
索亚历险记》共需![]() 元.
元.
![]() 求每本《汤姆
求每本《汤姆![]() 索亚历险记》和《童年》的定价各是多少元?
索亚历险记》和《童年》的定价各是多少元?
![]() 该校计划购买两种图书共
该校计划购买两种图书共![]() 本,并且要求《汤姆
本,并且要求《汤姆![]() 索亚历险记》的数量不少于《童年》数量的
索亚历险记》的数量不少于《童年》数量的![]() 倍,请你设计一种购买方案,使得购买两种图书所需的总费用最低.
倍,请你设计一种购买方案,使得购买两种图书所需的总费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.
(1)求证:AE与⊙O相切于点A;
(2)若AE∥BC,BC=2![]() ,AC=2
,AC=2![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长都为1,点A,点B在网格中的位置如图所示.
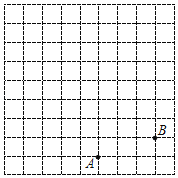
(1)建立适当的直角坐标系,使点A,点B的坐标分别为(1,﹣3),(4,﹣2);
(2)若点C的坐标为(﹣1,﹣1),在平面直角坐标系中画出△ABC;
(3)在图中作出△ABC关于x轴对称的图形△A1B1C1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() 中,
中,![]() ,点
,点![]() 在线段
在线段![]() 上运动(
上运动(![]() 不与
不与![]() 重合),连结
重合),连结![]() ,作
,作![]() ,
,![]() 交线段
交线段![]() 于点
于点![]() .
.
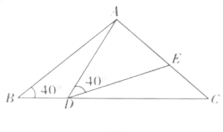
(1)当![]() 时,
时,![]() = °;点
= °;点![]() 从点
从点![]() 向点
向点![]() 运动时,
运动时,![]() 逐渐变 (填“大”或“小”);
逐渐变 (填“大”或“小”);
(2)当![]() 等于多少时,
等于多少时,![]() ,请说明理由;
,请说明理由;
(3)在点![]() 的运动过程中,
的运动过程中,![]() 的形状也在改变,判断当
的形状也在改变,判断当![]() 等于多少度时,
等于多少度时,![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与y轴交于点A,点B(-1,n)是该函数图象与反比例函数
的图象与y轴交于点A,点B(-1,n)是该函数图象与反比例函数![]() (k≠0)图象在第二象限内的交点.
(k≠0)图象在第二象限内的交点.
(1)求点B的坐标及k的值;
(2)试在x轴上确定点C,使AC=AB,请直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人走进一家商店,进门付l角钱,然后在店里购物花掉当时他手中钱的一半,走出商店付1角钱;之后,他走进第二家商店付1角钱,在店里花掉当时他手中钱的一半, 走出商店付1角钱;他又进第三家商店付l角钱,在店里花掉当时他手中钱的一半,出店付1角钱;最后他走进第四家商店付l角钱,在店里花掉当时他手中钱的一半, 出店付1角钱,这时他一分钱也没有了.该人原有钱的数目是________角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是 (把所有正确结论的序号都填在横线上)
(1)∠DCF=![]() ∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF
∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com