
分析 (1)根据绝对值的意义,分类讨论,可得答案;
(2)根据绝对值的意义,分类讨论,可得答案;
(3)根据绝对值的意义,分类讨论,可得答案;
(4)先求出在y2012这些不同的值中的最大值和最小值,再相减即可求解;
(5)根据观察,归纳,发现规律,可得答案.
解答 解:(1)x1<0时,y1=$\frac{{|{x_1}|}}{x_1}$=-1,x1>0时,y1=$\frac{{|{x_1}|}}{x_1}$=-1,则y1=±1;
(2)若x1>0,x2>0时,y2=$\frac{|{x}_{1}|}{{x}_{1}}$+$\frac{|{x}_{2}|}{{x}_{2}}$=2,
x1>0,x2<0时,y2=$\frac{|{x}_{1}|}{{x}_{1}}$+$\frac{|{x}_{2}|}{{x}_{2}}$=0,
x1<0,x2<0时,y2=$\frac{|{x}_{1}|}{{x}_{1}}$+$\frac{|{x}_{2}|}{{x}_{2}}$=-2,
综上所述,y2=±2或0;
(3)x1>0,x2>0,x3>0,y3=$\frac{|{x}_{1}|}{{x}_{1}}$+$\frac{|{x}_{2}|}{x2}$+$\frac{|{x}_{3}|}{{x}_{3}}$=3,
x1>0,x2>0,x3<0,y3=$\frac{|{x}_{1}|}{{x}_{1}}$+$\frac{|{x}_{2}|}{x2}$+$\frac{|{x}_{3}|}{{x}_{3}}$=1
x1>0,x2<0,x3<0,y3=$\frac{|{x}_{1}|}{{x}_{1}}$+$\frac{|{x}_{2}|}{x2}$+$\frac{|{x}_{3}|}{{x}_{3}}$=-1,
x1<0,x2<0,x3<0,y3=$\frac{|{x}_{1}|}{{x}_{1}}$+$\frac{|{x}_{2}|}{x2}$+$\frac{|{x}_{3}|}{{x}_{3}}$=-3
综上所述,y3=±1,±3;
(4)由以上探究可知,在y2012这些不同的值中,最大的值和最小的值的差等于2012-(-2012)=4024;
(5)由以上探究可知,y2012=$\frac{|{x}_{1}|}{{x}_{1}}$+$\frac{|{x}_{2}|}{{x}_{2}}$+…+$\frac{|{x}_{2012}|}{{x}_{2012}}$,则y2012共有2013个不同的值.
故答案为:±1;±2或0;±3或±1,4024;2013.
点评 本题考查了绝对值,利用了分类讨论的思想,发现规律是解题关键.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:选择题

| A. | $\frac{25}{8}$ | B. | $\frac{25}{16}$ | C. | $\frac{25}{4}$ | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
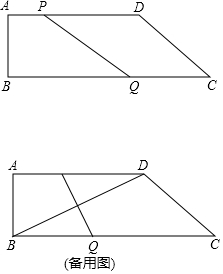 如图,在四边形ABCD中,AD‖BC,∠B=90°,AB=4cm,AD=8cm,BC=14cm,点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动,规定其中一个动点到达端点时,另一个端点也随之停止运动.
如图,在四边形ABCD中,AD‖BC,∠B=90°,AB=4cm,AD=8cm,BC=14cm,点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动,规定其中一个动点到达端点时,另一个端点也随之停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com