
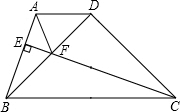
 如图,梯形ABCD中,AD∥BC,CE⊥AB于E,交梯形的对角线BD于F,连接AF.若△BDC为等腰直角三角形,且∠BDC=90°.
如图,梯形ABCD中,AD∥BC,CE⊥AB于E,交梯形的对角线BD于F,连接AF.若△BDC为等腰直角三角形,且∠BDC=90°.分析 作DH⊥AD交CE于H,如图,由AD∥BC得到DH⊥BC,根据等腰直角三角形的性质易得∠3=∠4=∠CDH=45°,CD=CB,则可证明△CDH≌△BDA得到CH=BA,DH=DA,接着证明△DHF≌△DAF得到FH=AF,于是有CF=CH+FH=AB+AF.
解答 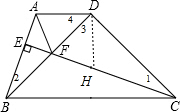 证明:作DH⊥AD交CE于H,如图,
证明:作DH⊥AD交CE于H,如图,
∵AD∥BC,
∴DH⊥BC,
∵△BDC为等腰直角三角形,
∴∠3=45°,BD=CD,
∴∠4=45°,
∴∠3=∠4=∠CDH,
∵CE⊥AB,
∴∠2+∠BFE=90°,
而∠1+∠DFC=90°,∠BFE=∠CFD,
∴∠1=∠2,
在△CDH和△BDA中,
$\left\{\begin{array}{l}{∠1=∠2}\\{CD=BA}\\{∠CDH=∠4}\end{array}\right.$,
∴△CDH≌△BDA(ASA),
∴CH=BA,DH=DA,
在△DHF和△DAF中
$\left\{\begin{array}{l}{DH=DA}\\{∠3=∠4}\\{DF=DF}\end{array}\right.$,
∴△DHF≌△DAF(SAS),
∴FH=AF,
∴CF=CH+FH=AB+AF.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.把CF分成两段,分别证明它们与AB和AF相等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
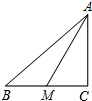 如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,cos∠CAM=$\frac{4}{5}$,则tan∠B的值为$\frac{2}{3}$.
如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,cos∠CAM=$\frac{4}{5}$,则tan∠B的值为$\frac{2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一个游戏的中奖概率是$\frac{1}{100}$,则做100次这样的游戏一定会中奖 | |
| B. | 为了解全国中学生的心理健康情况,应该采用普查的方式 | |
| C. | 一组数据 8,8,7,10,6,8,9 的众数和中位数都是8 | |
| D. | 若甲组数据的方差s2=0.01,乙组数据的方差s2=0.1,则乙组数据比甲组数据稳定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
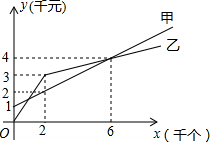 某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,
某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
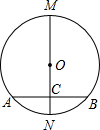 如图,在⊙O中,MN是直径,AB是弦,且MN⊥AB,垂足为C,下列结论:
如图,在⊙O中,MN是直径,AB是弦,且MN⊥AB,垂足为C,下列结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com