
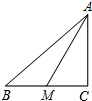
 如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,cos∠CAM=$\frac{4}{5}$,则tan∠B的值为$\frac{2}{3}$.
如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,cos∠CAM=$\frac{4}{5}$,则tan∠B的值为$\frac{2}{3}$. 分析 先在Rt△ACM中利用余弦定义得到cos∠CAM=$\frac{AC}{AM}$=$\frac{4}{5}$,则可设AC=4x,AM=5x,接着根据勾股定理可计算出CM=3x,所以BC=2CM=6x,然后在Rt△ABC中利用正切的定义求解.
解答 解:在Rt△ACM中,cos∠CAM=$\frac{AC}{AM}$=$\frac{4}{5}$,
设AC=4x,则AM=5x,
则CM=$\sqrt{A{M}^{2}-A{C}^{2}}$=3x,
而AM是BC边上的中线,
所以BC=2CM=6x,
在Rt△ABC中,tan∠B=$\frac{AC}{BC}$=$\frac{4x}{6x}$=$\frac{2}{3}$.
故答案为$\frac{2}{3}$.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.


科目:初中数学 来源:2016-2017学年度海南省九年级第二次月考数学试卷(解析版) 题型:解答题
如图,正方形ABCD中,点P是AD上的一动点(与点D、点A不重合),DE⊥CP,垂足为E,EF⊥BE与DC交于点F.
(1)求证:△DEF∽△CEB;
(2)当点P运动到DA的中点时,求证:点F为DC的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
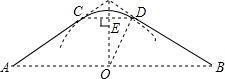 如图,某公园的一角有一块草坪(阴影部分),实线部分是沿草坪外围的一条小路,小路由两条相等的线段AC、BD和圆弧CD组成,其中AC、BD分别与圆弧CD相切于点C、D.经过测量,线段CD与半径OD都为60米,则这条小路的长度为120$\sqrt{3}$+2π米.
如图,某公园的一角有一块草坪(阴影部分),实线部分是沿草坪外围的一条小路,小路由两条相等的线段AC、BD和圆弧CD组成,其中AC、BD分别与圆弧CD相切于点C、D.经过测量,线段CD与半径OD都为60米,则这条小路的长度为120$\sqrt{3}$+2π米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 各类 | 频数 | 频率 |
| 卡通画 | a | 0.56 |
| 时文杂志 | 32 | b |
| 武侠小说 | 30 | 0.15 |
| 文学名著 | c | d |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
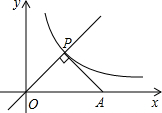 如图,点P是正比例函数y=x与反比例函数y=$\frac{k}{x}$在第一象限内的交点,PA⊥OP交x轴于点A,△POA的面积为3,则k的值是3.
如图,点P是正比例函数y=x与反比例函数y=$\frac{k}{x}$在第一象限内的交点,PA⊥OP交x轴于点A,△POA的面积为3,则k的值是3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
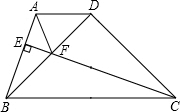 如图,梯形ABCD中,AD∥BC,CE⊥AB于E,交梯形的对角线BD于F,连接AF.若△BDC为等腰直角三角形,且∠BDC=90°.
如图,梯形ABCD中,AD∥BC,CE⊥AB于E,交梯形的对角线BD于F,连接AF.若△BDC为等腰直角三角形,且∠BDC=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com