
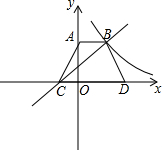
 如图,等腰梯形ABCD中,AB∥CD,AB=2,CD=4,A(0,3),直线y=ax+b过B、C两点,反比例函数y=
如图,等腰梯形ABCD中,AB∥CD,AB=2,CD=4,A(0,3),直线y=ax+b过B、C两点,反比例函数y=| k |
| x |
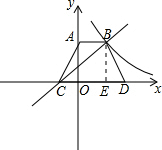 解:①过B作BE⊥x轴,与x轴交于E点,
解:①过B作BE⊥x轴,与x轴交于E点,
|
| 1 |
| 2 |
|
|
| 6 |
| x |


科目:初中数学 来源: 题型:
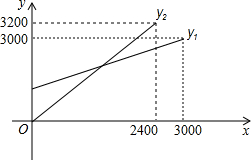 某单位急需用车,但又不准备买车,他们准备和一个体车主或一国有出租车公司签订月租车合同.设汽车每月行驶xkm,应付给个体车主的月费用为y1元,应付给国有出租车公司的月费用是y2元,y1、y2分别与x之间的函数关系图象(两条射线)如图所示,观察图象回答下列问题,问路程等于多少费用相等?费用是多少?
某单位急需用车,但又不准备买车,他们准备和一个体车主或一国有出租车公司签订月租车合同.设汽车每月行驶xkm,应付给个体车主的月费用为y1元,应付给国有出租车公司的月费用是y2元,y1、y2分别与x之间的函数关系图象(两条射线)如图所示,观察图象回答下列问题,问路程等于多少费用相等?费用是多少?查看答案和解析>>
科目:初中数学 来源: 题型:
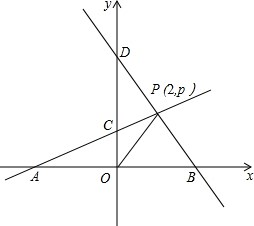 已知,A、B分别是x轴上位于原点左、右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,S△AOP=6.
已知,A、B分别是x轴上位于原点左、右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,S△AOP=6.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com