
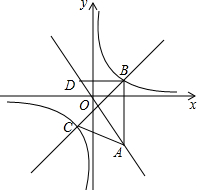
 如图,在平面直角坐标系xOy中,点A(a,-$\frac{7}{2}$)在直线y=-$\frac{3}{2}x-\frac{1}{2}$上,AB∥y轴,且点B的纵坐标为1,双曲线y=$\frac{m}{x}$经过点B.
如图,在平面直角坐标系xOy中,点A(a,-$\frac{7}{2}$)在直线y=-$\frac{3}{2}x-\frac{1}{2}$上,AB∥y轴,且点B的纵坐标为1,双曲线y=$\frac{m}{x}$经过点B.分析 (1)根据一次函数图象上点的坐标特征可得到-$\frac{3}{2}$a-$\frac{1}{2}$=$\frac{7}{2}$,解得a=2,则A(2,-$\frac{7}{2}$),再确定点B的坐标为(2,1),然后把B点坐标代入y=$\frac{m}{x}$中求出m的值即可得到反比例函数的解析式;
(2)①设C(t,$\frac{2}{t}$),根据三角形面积公式得到$\frac{1}{2}$×(2-t)×(1+$\frac{7}{2}$)=$\frac{27}{4}$,解得t=-1,则点C的坐标为(-1,-2),再利用待定系数法求直线BC的解析式;
②先确定D(-1,1),根据直线BC解析式的特征可得直线BC与x轴的夹角为45°,而BD∥x轴,于是得到∠DBC=45°,根据正方形的判定方法,只有△PBD为等腰直角三角形时,以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,分类讨论:若∠BPD=90°,则点P在BD的垂直平分线上,易得此时P($\frac{1}{2}$,-$\frac{1}{2}$);若∠BDP=90°,利用PD∥y轴,易得此时P(-1,-2).
解答 解:(1)∵点A(a,$-\frac{7}{2}$)在直线y=-$\frac{3}{2}x-\frac{1}{2}$上,
∴-$\frac{3}{2}$a-$\frac{1}{2}$=$\frac{7}{2}$,解得a=2,
则A(2,-$\frac{7}{2}$),
∵AB∥y轴,且点B的纵坐标为1,
∴点B的坐标为(2,1).
∵双曲线y=$\frac{m}{x}$经过点B(2,1),
∴m=2×1=2,
∴反比例函数的解析式为y=$\frac{2}{x}$;
(2)①设C(t,$\frac{2}{t}$),
∵A(2,-$\frac{7}{2}$),B(2,1),
∴$\frac{1}{2}$×(2-t)×(1+$\frac{7}{2}$)=$\frac{27}{4}$,
解得t=-1,
∴点C的坐标为(-1,-2),
设直线BC的解析式为y=kx+b,
把B(2,1),C(-1,-2)代入得$\left\{\begin{array}{l}{2k+b=1}\\{-k+b=-2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=-1}\end{array}\right.$,
∴直线BC的解析式为y=x-1;
②当y=1时,-$\frac{3}{2}x-\frac{1}{2}$=1,解得x=-1,则D(-1,1),
∵直线BCy=x-1为直线y=x向下平移1个单位得到,
∴直线BC与x轴的夹角为45°,
而BD∥x轴,
∴∠DBC=45°,
当△PBD为等腰直角三角形时,以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,
若∠BPD=90°,则点P在BD的垂直平分线上,P点的横坐标为$\frac{1}{2}$,当x=$\frac{1}{2}$时,y=x-1=-$\frac{1}{2}$,此时P($\frac{1}{2}$,-$\frac{1}{2}$),
若∠BDP=90°,则PD∥y轴,P点的横坐标为-1,当x=-1时,y=x-1=-2,此时P(-1,-2),
综上所述,满足条件的P点坐标为(-1,-2)或($\frac{1}{2}$,$-\frac{1}{2}$).
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了待定系数法求函数解析式和正方形的判定方法.


科目:初中数学 来源: 题型:选择题
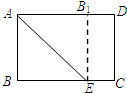 如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )
如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )| A. | 1cm | B. | 2cm | C. | 4cm | D. | 6cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC的顶点都在每个边长为1个单位长度的方格纸的格点上,将△ABC向右平移3格,再向上平移2格.
如图,△ABC的顶点都在每个边长为1个单位长度的方格纸的格点上,将△ABC向右平移3格,再向上平移2格.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com