
����Ŀ����ͼ����Rt��ABC�У���ACB��90����AC��6cm��BC��8cm����P�ӵ�A�������߶�AB��ÿ��1cm���ٶ��˶���ͬʱ��Q�ӵ�B����������B��C��A��ÿ��2cm���ٶ��˶�������һ��ֹͣ����һ��Ҳ��ֹ֮ͣ�����˶�ʱ��Ϊt�룮
��������ֱ��д��t��ȡֵ��Χ���� ����
�ڵ���P�˶���AB�е�ʱ������PQ��PC��BQ����֤����CPQ�ס�ABQ��
����������BPQ��ֱ��������ʱ����t��ֵ��
���𰸡���������0��t��7���ڼ�������������t��![]() ��
��![]()
��������
�����������ù��ɶ������AB�ij����ɽ�����⣮
���������Ƕ�Ӧ��������������Ƽ���֤����
���������������Σ�����ͼ2�У���PQ��ACʱ����PQB����C��90��������ͼ3�У�����QPB��90��ʱ���ֱ���⼴�ɣ�
���������⣺��Rt��ABC�У��ߡ�ACB��90����AC��6��BC��8��
��AB��![]() ��
��![]() ��10��
��10��
��![]() ��10��
��10��![]() ��7��7��10��
��7��7��10��
��t��ȡֵ��ΧΪ��![]() ��
��
�ʴ�Ϊ��0��t��7��
��֤������ͼ1�У��������P�˶���AB���е�ʱ��t��5��
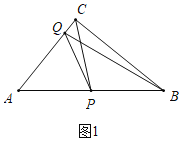
��CQ��5��2��8��2��
�ߡ�ACB��90����PA��PB��
��PC��PA��PB��5��
���PCQ����A��
��![]() ��
��![]() ��
��
��![]() ��
��
���QCP�ס�CAB��
�������⣺����ͼ2�У���PQ��ACʱ����PQB����C��90����
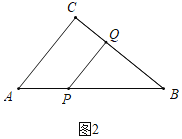
��PQ��AC��
��![]() ��
��
��![]() ��
��
��ã�![]() ��
��
����ͼ3�У�����QPB��90��ʱ��
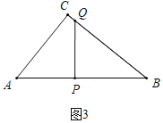
�ߡ�QPB����ACB��90������B����B��
���BPQ�ס�BCA��
��![]() ��
��
��![]() ��
��
��ã�![]() ��
��
��������������������t��ֵΪ��![]() ��
��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ��ʾ����֪���κ���![]() ��ͼ�����þ�������ԭ�㣬�Գ���Ϊֱ��
��ͼ�����þ�������ԭ�㣬�Գ���Ϊֱ��![]() .���������ĸ�����:��
.���������ĸ�����:��![]() ����
����![]() ����
����![]() ����
����![]() .��ȷ���У� ��
.��ȷ���У� ��

A.![]() ��B.
��B.![]() ��C.
��C.![]() ��D.
��D.![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ��� (m-1)x![]() -mx+1=0��
-mx+1=0��
��1��֤��������mΪ��ֵʱ����������ʵ������
��2����mΪ��������mΪ��ֵʱ����������������ȵ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ڽ��ڡ�O��AD��BC��OE��BC������BAC��45����
��1����֤��OE��![]() BC��
BC��
��2������ACD��AC�۵�Ϊ��ACF������ABD��AB�۵�Ϊ��ABG���ӳ�FC��GB�ཻ�ڵ�H����BD��6��CD��4����AD�ij���
��3����OM��AB��M��ON��AC��N���ڣ�2������������![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O������O��һ��ֱ�߷ֱ�DA��BC���ӳ����ڵ�E��F������BE��DF��
��1����֤���ı���BFDE��ƽ���ı��Σ�
��2����EF��AB������ΪM��![]() ��AE��2��������ABCD�ı߳���
��AE��2��������ABCD�ı߳���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���������Ϊ30Ԫ��̨����40Ԫ�ļ۸��۳���ƽ��ÿ�����۳�600�������������������̨�Ƶ��ۼ�ÿ����1Ԫ���������ͼ���10�����г��涨��̨���ۼ۲��ó���60Ԫ��Ϊ��ʵ����������̨��ƽ��ÿ��10000Ԫ�����������ۼ�Ӧ��Ϊ����Ԫ����ʱ�۳�̨�ƶ��ٸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��HW��˾2018��ʹ�������з������ġ�QL��ϵ�мס��ҡ�������оƬ��2800��飬������2800���ֻ�����������оƬ�IJ����Ǽ���оƬ��2��������оƬ�IJ����ȼף�������оƬ�����ĺͻ���400��飮��Щ��QL��оƬ����˸ù�˾2018��������ȫ���ֻ�����оƬ��10%��
��1����2018�����оƬ�IJ�����
��2��HW��˾�ƻ�2020���������ֻ�ȫ��ʹ�������з��ġ�QL��ϵ��оƬ����2019������������QL��оƬ�IJ�����2019�ꡢ2020�������꣬����оƬÿ��IJ�������ǰһ������һ����ͬ�İٷ���m%������оƬ�IJ���ƽ��ÿ�������İٷ�����m%С1%������оƬ�IJ���ÿ�갴��ͬ������3200��������������2020���HW��˾���ֻ�������2018��ȫ����ֻ�������10%����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
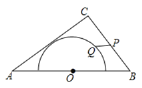
����Ŀ����ͼ,��![]() �У�
�У�![]() ,�Ա�
,�Ա�![]() ���е�
���е�![]() ΪԲ��,����Բ��
ΪԲ��,����Բ��![]() ���У���
���У���![]() �ֱ��DZ�
�ֱ��DZ�![]() �Ͱ�Բ�ϵĶ���,����
�Ͱ�Բ�ϵĶ���,����![]() ,��
,��![]() �������ֵ����Сֵ�ĺ��ǣ� ��
�������ֵ����Сֵ�ĺ��ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������y=mx2��2mx��3��m��0����x�ύ��A��3��0����B���㣮
��1���������ߵı���ʽ����B�����ꣻ
��2������2��x��3ʱ�ĺ���ͼ���ΪG�����ʱ����y��ȡֵ��Χ��
��3���ڣ�2���������£���ͼ��G��x���Ϸ��IJ�����x�ᷭ�ۣ�ͼ��G�����ಿ�ֱ��ֲ��䣬�õ�һ����ͼ��M����������C��4.2����ֱ��y=kx+b��k��0����ͼ��M�ڵ��������������������㣬���ͼ����b��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com