
已知等差数列 的公差
的公差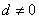 ,它的前
,它的前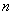 项和为
项和为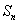 ,若
,若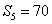 ,且
,且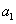 ,
,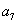 ,
,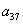 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)设数列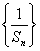 的前
的前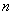 项和为
项和为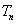 ,求证:
,求证: .
.
(1)解:因为数列 是等差数列,
是等差数列,
所以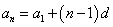 ,
,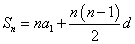 . …………………………………1分
. …………………………………1分
依题意,有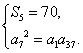 即
即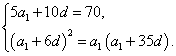 …………………3分
…………………3分
解得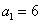 ,
,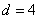 . ………………………………………………………………5分
. ………………………………………………………………5分
所以数列 的通项公式为
的通项公式为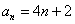 (
(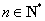 ). …………………………6分
). …………………………6分
(2)证明:由(1)可得
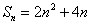 . …………………………………………7分
. …………………………………………7分
所以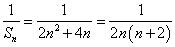
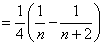 . …………………………8分
. …………………………8分
所以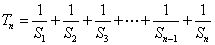
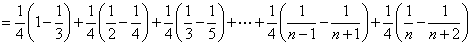 ……9分
……9分
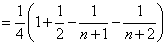
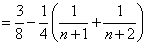 . …………………………………………………10分
. …………………………………………………10分
因为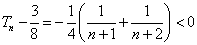 ,所以
,所以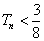 . …………………………11分
. …………………………11分
因为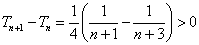 ,
, 所以数列
所以数列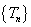 是递增数列. …………12分
是递增数列. …………12分
所以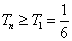 . …………………………………………………………………13分
. …………………………………………………………………13分
所以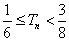 . …………………………………………………………………14分
. …………………………………………………………………14分


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
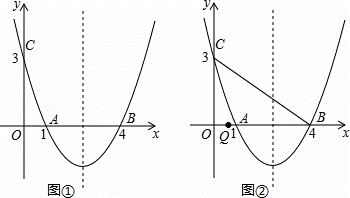
如图,抛物线y=ax2+bx+c经过A(1,0)、B(4,0)、C(0,3)三点.
(1)求抛物线的解析式;
(2)如图①,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.
(3)如图②,点Q是线段OB上一动点,连接BC,在线段BC上是否存在这样的点M,使△CQM为等腰三角形且△BQM为直角三角形?若存在,求点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
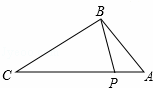
如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A. ∠ABP=∠C B. ∠APB=∠ABC C.  =
=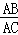 D.
D. 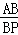 =
=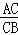
查看答案和解析>>
科目:初中数学 来源: 题型:
清明期间,某校师生组成200个小组参加“保护环境,美化家园”植树活动.综合实际情况,校方要求每小组植树量为2至5棵,活动结束后,校方随机抽查了其中50个小组,根据他们的植树量绘制出如图所示的两幅不完整统计图.请根据图中提供的信息,解答下面的问题:
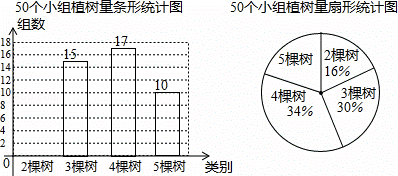
(1)请把条形统计图补充完整,并算出扇形统计图中,植树量为“5棵树”的圆心角是 72 °.
(2)请你帮学校估算此次活动共种多少棵树.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com