
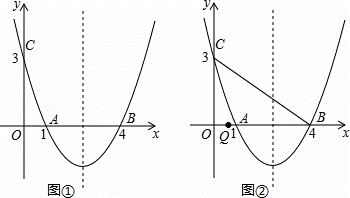
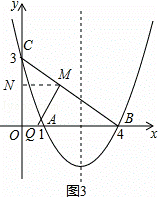
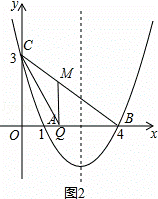
如图,抛物线y=ax2+bx+c经过A(1,0)、B(4,0)、C(0,3)三点.
(1)求抛物线的解析式;
(2)如图①,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.
(3)如图②,点Q是线段OB上一动点,连接BC,在线段BC上是否存在这样的点M,使△CQM为等腰三角形且△BQM为直角三角形?若存在,求点M的坐标;若不存在,请说明理由.
解:(1)由已知得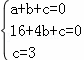 解得
解得 .
.
所以,抛物线的解析式为y=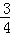 x2﹣
x2﹣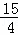 x+3.
x+3.
(2)∵A、B关于对称轴对称,如图1,连接BC,
∴BC与对称轴的交点即为所求的点P,此时PA+PC=BC,
∴四边形PAOC的周长最小值为:OC+OA+BC,
∵A(1,0)、B(4,0)、C(0,3),
∴OA=1,OC=3,BC=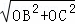 =5,
=5,
∴OC+OA+BC=1+3+5=9;
∴在抛物线的对称轴上存在点P,使得四边形PAOC的周长最小,四边形PAOC周长的最小值为9.
(3)∵B(4,0)、C(0,3),
∴直线BC的解析式为y=﹣ x+3,
x+3,
①当∠BQM=90°时,如图2,设M(a,b),
∵∠CMQ>90°,
∴只能CM=MQ=b,
∵MQ∥y轴,
∴△MQB∽△COB,
∴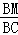 =
=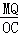 ,即
,即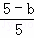 =
=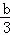 ,解得b=
,解得b= ,代入y=﹣
,代入y=﹣ x+3得,
x+3得, =﹣
=﹣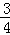 a+3
a+3 ,解得a=
,解得a=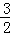 ,
,
∴M(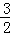 ,
,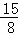 );
);
②当∠QMB=90°时,如图3,
∵∠CMQ=90°,
∴只能CM=MQ,
设CM=MQ=m,
∴BM=5﹣m,
∵∠BMQ=∠COB=90°,∠MBQ=∠OBC,
∴△BMQ∽△BOC,
∴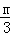 =
=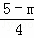 ,解得m=
,解得m=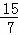 ,
,
作MN∥OB,
∴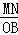 =
=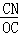 =
= ,即
,即 =
=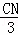 =
=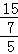 ,
,
∴MN=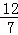 ,CN=
,CN=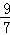 ,
,
∴ON=OC﹣CN=3﹣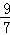 =
=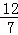 ,
,
∴M(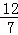 ,
,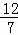 ),
),
综上,在线段BC上存在这样的点M,使△CQM为等腰三角形且△BQM为直角三角形,点M的坐标为(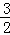 ,
,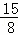 )或(
)或(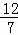 ,
,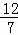 ).
).



 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
下列四个立体图形中,它们各自的三视图有两个相同,而另一个不同的是(  )
)

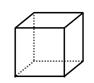
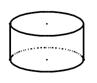

① 球 ② 正方体 ③ 圆柱 ④ 圆锥
A.①② B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
已知反比例函数y=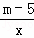 (m为常数,且m≠5).
(m为常数,且m≠5).
(1)若在其图象的每个分支上,y随x的增大而增大,求m的取值范围;
(2)若其图象与一次函数y=﹣x+1图象的一个交点的纵坐标是3,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
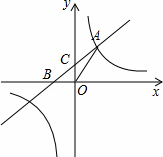
如图,直线y=x+b与双曲线y=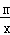 都经过点A(2,3),直线y=x+b与x轴、y轴分别交于B、C两点.
都经过点A(2,3),直线y=x+b与x轴、y轴分别交于B、C两点.
(1)求直线和双曲线的函数关系式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知实数a,b在数轴上的位置如图所示,下列结论错误的是( )

|
| A. | |a|<1<|b| | B. | 1<﹣a<b | C. | 1<|a|<b | D. | ﹣b<a<﹣1 |

查看答案和解析>>
科目:初中数学 来源: 题型:
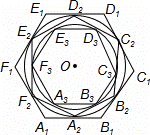
如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
|
| A. |
| B. |
| C. |
| D. |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙、丙、丁四人参加训练,近期的10次百米测试平均成绩都是13.2秒,方差如表
| 选手 | 甲 | 乙 | 丙 | 丁 |
| 方差(秒2) | 0.020 | 0.019 | 0.021 | 0.022 |
则这四人中发挥最稳定的是( )
|
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com