
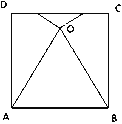
【题目】如图,将正方形ABCD的边AD和边BC折叠,使点C与点D重合于正方形内部一点O,已知点O到边CD的距离为a,则点O到边AB的距离为 .(用a的代数式表示)
【答案】(3+2![]() )a.
)a.
【解析】
试题分析:本题考查的是翻转变换的性质和等边三角形的性质,翻转变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.作OG⊥CD于G,交AB于H,根据翻转变换的性质得到OA=AD,OB=BC,∠EOA=∠D=90°,∠FOB=∠C=90°,根据直角三角形的性质和勾股定理求出DE、EF、FC,得到正方形的边长,计算即可.
作OG⊥CD于G,交AB于H,
∵CD∥AB,
∴OH⊥AB于H,
由翻转变换的性质可知,OA=AD,OB=BC,∠EOA=∠D=90°,∠FOB=∠C=90°,
∴△OAB是等边三角形,∠EOF=120°,
∴∠OEF=30°,
∴EO=2a,EG=![]() a,
a,
∴DE=OE=2a,OF=FC=2a,EF=2EG=2![]() a,
a,
∴DC=4a+2![]() a,
a,
∴点O到边AB的距离为4a+2![]() a-a=3a+2
a-a=3a+2![]() a=(3+2
a=(3+2![]() )a.
)a.
故答案为(3+2![]() )a.
)a.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标为(3,4),则A关于x轴对称的点的坐标是( )
A. (-3,4) B. (3,-4) C. (-3,-4) D. (4,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
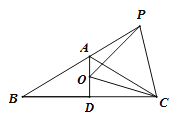
【题目】等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,以下结论:①∠APO=∠DCO; ②∠APO+∠DCO=30°;③△OPC为等边三角形;④AC=AD+AP;⑤![]() . 其中正确的有( )
. 其中正确的有( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC,∠BAC=120°,点D为AB中点,点E在BC边上,CE=3BE,AE与CD交于点F, 若AF=![]() ,则FC的长为________________.
,则FC的长为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
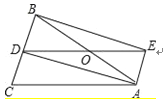
【题目】如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com