
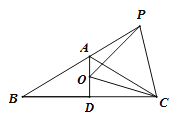
【题目】等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,以下结论:①∠APO=∠DCO; ②∠APO+∠DCO=30°;③△OPC为等边三角形;④AC=AD+AP;⑤![]() . 其中正确的有( )
. 其中正确的有( )
A. 2个 B. 3个 C. 4个 D. 5个
【答案】B
【解析】如图,
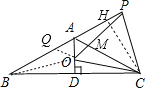
①连接OB,
∵AB=AC,BD=CD,
∴AD是BC垂直平分线,
∴OB=OC=OP,
∴∠APO=∠ABO,∠DBO=∠DCO,
∵∠ABO+∠DBO=30°,
∴∠APO+∠DCO=30°.故①正确;
②∵△OBP中,∠BOP=180°∠OPB∠OBP,
△BOC中,∠BOC=180°∠OBC∠OCB,
∴∠POC=360°∠BOP∠BOC=∠OPB+∠OBP+∠OBC+∠OCB,
∵∠OPB=∠OBP,∠OBC=∠OCB,
∴∠POC=2∠ABD=60°,
∵PO=OC,
∴△OPC是等边三角形,故②正确;
③在AB上找到Q点使得AQ=OA,则△AOQ为等边三角形,
则∠BQO=∠PAO=120°,
在△BQO和△PAO中,
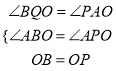
∴△BQO≌△PAO(AAS),
∴PA=BQ,
∵AB=BQ+AQ,
∴AC=AO+AP,故③正确;
④作CH⊥CD,

∵∠HCB=60,∠PCO=60,
∴∠PCH=∠OCD,
在△CDO和△CHP中,
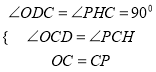
∴△CDO≌△CHP(AAS),
∴S△OCD=S△CHP
∴CH=CD,
∵CD=BD,
∴BD=CH,
在RT△ABD和RT△ACH中,
![]()
∴RT△ABD≌RT△ACH(HL),
∴S△ABD=S△AHC,
∵四边形OAPC面积=S△OAC+S△AHC+S△CHP,S△ABC=S△AOC+S△ABD+S△OCD
∴四边形OAPC面积=S△ABC.故④正确。
故选B.


科目:初中数学 来源: 题型:
【题目】甲、乙两商场自行定价销售某一商品.
(1)甲商场将该商品提价25%后的售价为1.25元,则该商品在甲商场的原价为 元;
(2)乙商场定价有两种方案:方案将该商品提价20%;方案将该商品提价1元。某顾客发现在乙商场用60元钱购买该商品,按方案购买的件数是按方案购买的件数的2倍少10件,求该商品在乙商场的原价是多少?
(3)甲、乙两商场把该商品均按原价进行了两次价格调整.甲商场:第一次提价的百分率是a,第二次提价的百分率是b;乙商场:两次提价的百分率都是![]() (a>0,b>0,a≠b).请问甲、乙两商场,哪个商场的提价较多?请说明理由.
(a>0,b>0,a≠b).请问甲、乙两商场,哪个商场的提价较多?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司去年1-3月平均亏损1.5万元,4-6月平均盈利2万元,7-10月平均每月盈利1.7万元,11-12月平均每月亏损2.3万元,这个公司去年盈亏情况是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将正方形ABCD的边AD和边BC折叠,使点C与点D重合于正方形内部一点O,已知点O到边CD的距离为a,则点O到边AB的距离为 .(用a的代数式表示)
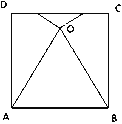
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律:71=7,72=49,73=343,74=2401,75=16807,…那么72007+1的个位数字是( )
A. 8 B. 4 C. 2 D. 0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是关于x的函数,且x,y满足方程组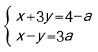 .
.
(1)求函数y的表达式;
(2)若点P的坐标为(m,0),求以P为圆心、1为半径的圆与函数y的图象有交点时,m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家鞋店对上一周某品牌女鞋的销量统计如下:
尺码(厘米) | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 |
销量(双) | 1 | 2 | 5 | 11 | 7 | 3 | 1 |
该店决定本周进货时,多进一些尺码为23.5厘米的鞋,影响鞋店决策的统计量是___________ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com