
【题目】已知y是关于x的函数,且x,y满足方程组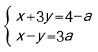 .
.
(1)求函数y的表达式;
(2)若点P的坐标为(m,0),求以P为圆心、1为半径的圆与函数y的图象有交点时,m的取值范围.
【答案】(1)y=-![]() x+
x+![]() ;(2)3-
;(2)3-![]() ≤m≤3+
≤m≤3+![]() .
.
【解析】
试题分析:本题考查直线和圆的位置关系、一次函数和坐标轴的交点、相似三角形的判定和性质以及切线的性质,题目的综合性较强,难度中等,是一道不错的中考题.
(1)把a作为已知数,分别得到x、y和a的数量关系即可求出函数y的表达式;
(2)易求点A和点B的坐标,当圆P与直线y相切时,设切点为C,则PC⊥直线y,求出此时P的横坐标即可得到函数y的图象有交点时,m的取值范围.
试题解析:(1)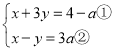 ,
,
①×3,得3x+9y=12-3a③
②+③,得4x+8y=12,即x+2y=3,
得,y=-![]() x+
x+![]() ;
;
(2)当y=0时,x=3,即函数y的图象与x轴交于点A(3,0).
当x=0时,y=![]() ,即函数y的图象与y轴交于点B(0,
,即函数y的图象与y轴交于点B(0,![]() ),
),
当圆P与直线y相切时,设切点为C,则PC![]() 直线y,
直线y,
此时∠PCA=90°,
∴∠PCA=∠BOA,
且∠BAO=∠PAC,
∴△ABO∽△APC,
∴![]() ,即
,即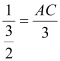 ,
,
∴AC=2,
∴PA=![]() ,
,
此时,P的横坐标为3-![]() 或3+
或3+![]() ,
,
∴当圆P与直线y有交点时,3-![]() ≤m≤3+
≤m≤3+![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
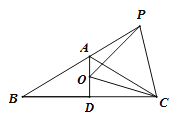
【题目】等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,以下结论:①∠APO=∠DCO; ②∠APO+∠DCO=30°;③△OPC为等边三角形;④AC=AD+AP;⑤![]() . 其中正确的有( )
. 其中正确的有( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC,∠BAC=120°,点D为AB中点,点E在BC边上,CE=3BE,AE与CD交于点F, 若AF=![]() ,则FC的长为________________.
,则FC的长为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据报道2018年4月,某市土地出让金达11.9亿,比2017年同期的7.984亿上涨幅度达到48.8%,其中数值11.9亿可用科学记数法表示为( )
A. 1.19×109 B. 11.9×108 C. 1.19×1010 D. 11.9×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
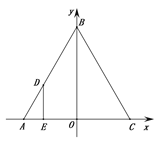
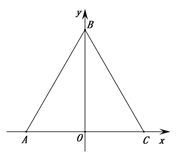
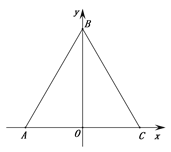
【题目】如图,等边△ABC的边AC在x轴上,AC中点O为坐标原点,已知C(2,0),动点D从A出发沿线段AB向终点B运动,速度为2个单位长度/秒,运动时间为t,过点D作DE⊥AC,垂足为E.
(1)当OD⊥AB时,求E点坐标.
(2)过E做EF⊥BC,垂足为F,过F作FG⊥AB,垂足为G,请用含t的式子表示线段DG的长度.
(3)在(2)的条件下,作点C关于EF的对称点H,连接HG并延长交直线DE于点Q,当t为何值时,HQ=EQ,并求出此时DG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
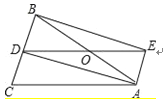
【题目】如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若某次数学考试标准成绩定为85分,规定高于标准记为正,两位学生的成绩分别记作:+9分和-3分,则第一位学生的实际得分为___________分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com