Question

13．某班共有52名同学，在校广播操比赛中排成方队，先把每位同学都进行编号，然后把各自的位置固定下来，如图，在平面直角坐标系中，每个自然数都对应着一个坐标．例如1的对应点是原点（0，0），3的对应点是（1，1），16的对应点是（-1，2）．那么最后一名同学的位置对应的坐标是（4，-1），全校学生如果排成这样一个大方阵，编号是2015的学生的对应点的坐标是（12，-22）．

Answer 1

分析 观察图的结构，发现所有奇数的平方数都在第四象限的角平分线上．依此先确定2025的坐标为（22，-22），再根据图的结构求得2015的坐标．

解答 解：观察图的结构，发现所有奇数的平方数都在第四象限的角平分线上．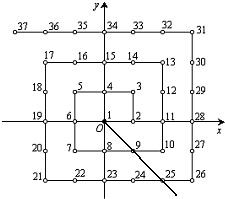
因为49=7²，7=2×3+1，
所以49的坐标是（3，-3），
所以52的坐标是（4，-1），
因为45²=2025，
由2n+1=45得n=22，
所以2025的坐标为（22，-22）．
因为2015=2025-10，
所以22-10=12，
所以2015的坐标是（12，-22）．
故答案为：（4，-1），（12，-22）．

点评 本题考查了点的坐标，找到所有奇数的平方数所在位置是解题的关键．