
分析 (1)利用抛物线对称轴方程易得抛物线的对称轴为直线x=1,然后根据抛物线的对称性可确定B(3,0);
(2)设抛物线解析式为y=a(x+1)(x-3),然后分别把C(0,3)和(0,-3)代入求出对应的a的值即可得到抛物线解析式;
(3)如图,先证明Rt△AOC∽△COB,利用相似比可计算出OC=$\sqrt{3}$,则C(0,$\sqrt{3}$)或(0,-$\sqrt{3}$),然后与(2)的求法一样.
解答 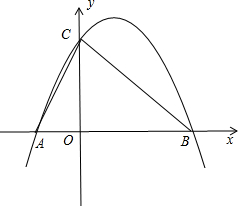 解:(1)抛物线的对称轴为直线x=-$\frac{-2a}{2a}$=1,
解:(1)抛物线的对称轴为直线x=-$\frac{-2a}{2a}$=1,
∵点A与点B为抛物线上的对称点,
∴B(3,0);
(2)∵OC=3,
∴C(0,3)或(0,-3),
设抛物线解析式为y=a(x+1)(x-3),
当C点坐标为(0,3)时,a•1•(-3)=3,解得a=-1,此时抛物线解析式为y=-(x+1)(x-3),即y=-x2+2x+3;
当C点坐标为(0,-3)时,a•1•(-3)=-3,解得a=1,此时抛物线解析式为y=(x+1)(x-3),即y=x2-2x-3;
(3)如图,
∵∠ACB=90°,即∠ACO+∠BCO=90°,
而∠ACO+∠OAC=90°,
∴∠OAC=∠OCB,
∴Rt△AOC∽△COB,
∴$\frac{OA}{OC}$=$\frac{OC}{OB}$,即$\frac{1}{OC}$=$\frac{OC}{3}$,解得OC=$\sqrt{3}$,
∴C(0,$\sqrt{3}$)或(0,-$\sqrt{3}$),
设抛物线解析式为y=a(x+1)(x-3),
当C点坐标为(0,$\sqrt{3}$)时,a•1•(-3)=$\sqrt{3}$,解得a=-$\frac{\sqrt{3}}{3}$,此时抛物线解析式为y=-$\frac{\sqrt{3}}{3}$(x+1)(x-3),即y=-$\frac{\sqrt{3}}{3}$x2+$\frac{2\sqrt{3}}{3}$x+$\sqrt{3}$;
当C点坐标为(0,-$\sqrt{3}$)时,a•1•(-3)=-$\sqrt{3}$,解得a=$\frac{\sqrt{3}}{3}$,此时抛物线解析式为y=$\frac{\sqrt{3}}{3}$(x+1)(x-3),即y=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x-$\sqrt{3}$.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标转化为解关于x的一元二次方程;从二次函数的交点式:y=a(x-x1)(x-x2)(a,b,c是常数,a≠0)中可直接得到抛物线与x轴的交点坐标(x1,0),(x2,0).也考查了待定系数法求抛物线解析式和相似三角形的判定与性质.


科目:初中数学 来源:2016-2017学年广西南宁市七年级下学期第一次月考数学试卷(解析版) 题型:解答题
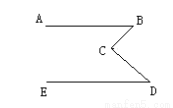
如图所示,AB∥ED,∠B=48º,∠D=42º,BC垂直于CD吗?如果垂直请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某班共有52名同学,在校广播操比赛中排成方队,先把每位同学都进行编号,然后把各自的位置固定下来,如图,在平面直角坐标系中,每个自然数都对应着一个坐标.例如1的对应点是原点(0,0),3的对应点是(1,1),16的对应点是(-1,2).那么最后一名同学的位置对应的坐标是(4,-1),全校学生如果排成这样一个大方阵,编号是2015的学生的对应点的坐标是(12,-22).
某班共有52名同学,在校广播操比赛中排成方队,先把每位同学都进行编号,然后把各自的位置固定下来,如图,在平面直角坐标系中,每个自然数都对应着一个坐标.例如1的对应点是原点(0,0),3的对应点是(1,1),16的对应点是(-1,2).那么最后一名同学的位置对应的坐标是(4,-1),全校学生如果排成这样一个大方阵,编号是2015的学生的对应点的坐标是(12,-22).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如果将点P绕定点M旋转180°后与点Q重合,那么点P与点Q关于点M对称,定点M叫做对称中心,此时,点M是线段PQ的中点,如图,在直角坐标系中,△ABO的顶点A、B、O的坐标分别为(1,0),(0,1),(0,0),点列P1、P2、P3…中的相邻两点都关于△ABO的一个顶点对称,点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与点P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称,且这些对称中心依次循环,已知点P1的坐标是(1,1),则点P2015的坐标为(1,3).
如果将点P绕定点M旋转180°后与点Q重合,那么点P与点Q关于点M对称,定点M叫做对称中心,此时,点M是线段PQ的中点,如图,在直角坐标系中,△ABO的顶点A、B、O的坐标分别为(1,0),(0,1),(0,0),点列P1、P2、P3…中的相邻两点都关于△ABO的一个顶点对称,点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与点P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称,且这些对称中心依次循环,已知点P1的坐标是(1,1),则点P2015的坐标为(1,3).查看答案和解析>>
科目:初中数学 来源:2016-2017学年重庆市校七年级下学期第一阶段考试数学试卷(解析版) 题型:填空题
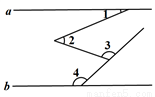
已知,如图,直线a∥b,则∠1、∠2、∠3、∠4之间的数量关系为__________________
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| a | 5 | 4 | -2 | -3 | 2 | |
| b | 3 | 0 | -1 | 0 | -4 | |
| A、B两点间的距离 | 2 | 3 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com