
分析 (1)根据△=b2-4ac决定抛物线与x轴的交点个数,计算判别式的值,然后利用非负数的性质说明判别式为非负数即可;
(2)先解方程mx2+(m-6)x-6=0得到抛物线与x轴的交点坐标为(-1,0),($\frac{6}{m}$,0),则根据题意得到|$\frac{6}{m}$+1|=2,然后解绝对值方程求出m即可.
解答 (1)证明:△=(m-6)2-4m•(-6)
=m2-12m+36+24m
=(m+6)2,
∵(m+6)2,≥0,即△≥0,
∴无论非零常数m为何值时,抛物线与x轴总有公共点;
(2)解:当y=0时,mx2+(m-6)x-6=0,
则x=$\frac{-(m-6)±\sqrt{(m+6)^{2}}}{2m}$=$\frac{-m+6±(m+6)}{2m}$,
解得x1=-1,x2=$\frac{6}{m}$,
∴抛物线与x轴的交点坐标为(-1,0),($\frac{6}{m}$,0),
∵抛物线与x轴的两个交点的距离等于2,
∴|$\frac{6}{m}$+1|=2,
解得m=6或m=-2,
即m为6或-2时,抛物线与x轴的两个交点的距离等于2.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的方程ax2+bx+c=0;=对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 10cm | B. | 10$\sqrt{3}$cm | C. | 20$\sqrt{3}$cm | D. | 5$\sqrt{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
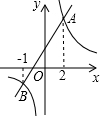 如图,一次函数y=kx+b(k、b为常数,且k≠0)的图象与反比例函数y=$\frac{m}{x}$(m为常数,且m≠0)的图象交于A、B两点.则关于x的方程kx+b=$\frac{m}{x}$的解为-1和2.
如图,一次函数y=kx+b(k、b为常数,且k≠0)的图象与反比例函数y=$\frac{m}{x}$(m为常数,且m≠0)的图象交于A、B两点.则关于x的方程kx+b=$\frac{m}{x}$的解为-1和2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
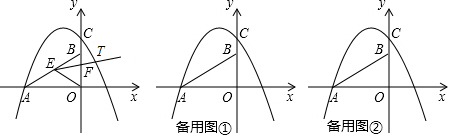
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
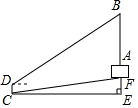 数学活动课上,老师和学生一起去侧量学校升旗台上旗杆AB的高度,如图,老师测得升旗台前斜坡FC的坡度为1:10(即EF:CE=1:10),学生吴昊站在离旗杆水平距离为27m(即CE=27m)的点C处,测得旗杆顶端B的仰角为30°,吴昊身高CD=1.6m,升旗台AF的高1.8m,请帮同学计算出旗杆AB的高度(结果精确到0.1米,$\sqrt{3}$≈1.73).
数学活动课上,老师和学生一起去侧量学校升旗台上旗杆AB的高度,如图,老师测得升旗台前斜坡FC的坡度为1:10(即EF:CE=1:10),学生吴昊站在离旗杆水平距离为27m(即CE=27m)的点C处,测得旗杆顶端B的仰角为30°,吴昊身高CD=1.6m,升旗台AF的高1.8m,请帮同学计算出旗杆AB的高度(结果精确到0.1米,$\sqrt{3}$≈1.73).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com