
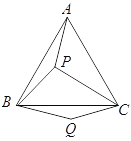
【题目】如图, ![]() 是等边三角形
是等边三角形![]() 内的一点,连结
内的一点,连结![]() 、
、![]() 、
、![]() ,以
,以![]() 为边作
为边作![]() 且
且![]() .连结
.连结![]() .
.
(1)观察并猜想![]() 与
与![]() 之间的大小关系,并证明你的结论.
之间的大小关系,并证明你的结论.
(2)若![]() ,
, ![]() ,
, ![]() ,连结
,连结![]() ,试判断
,试判断![]() 的形状,并说明理由.
的形状,并说明理由.
(3)在(2)的条件下,求![]() 的面积.
的面积.
【答案】(![]() )
)![]() ,证明见解析;(
,证明见解析;(![]() )
)![]() 为直角三角形,理由见解析;(
为直角三角形,理由见解析;(![]() )
)![]() .
.
【解析】试题分析:(1)通过证明△ABP≌△CBQ得出;(2)根据△BPQ是等边三角形求出PQ的长,再根据勾股定理逆定理可得△PQC是直角三角形;(3)过点B作BD垂直于CQ的延长线于点D,在△BDQ中求出DQ、BD的长,再求出CD,根据勾股定理求出BC的长,即可求出三角形ABC面积.
解:(1)AP=CQ,
理由:∵∠PBQ=60°,∠ABC=60°,
∴∠ABP+∠PBC=60°=∠CBQ+∠PBC,
∴∠ABP=∠CBQ,
在△ABP与△CBQ中,AB=CB,∠ABP=∠CBQ,BP=BQ,
∴△ABP≌△CBQ,
∴AP=CQ.
(2)∵BP=BQ,∠PBQ=60°,
∴△BPQ为等边三角形,
∴PQ=PB=4,
∵△ABP≌△CBQ,∴AP=CQ=3,
∵PQ2+CQ2=42+32=25=PC2,
∴△PQC为直角三角形.
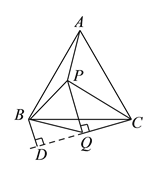
(3)∵∠PQC=90°,∠PQB=60°,
∴∠BQC=150°,
过点B作BD垂直于CQ的延长线于点D,
∴∠BQD=30°,
∵BQ=4,∴BD=2,DQ=2![]() ,
,
∴CD=CQ+DQ=3+![]() ,
,
在Rt△BCD中,BC=![]() ,
,
∵△ABC为等边三角形,
∴S△ABC=![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】对下列多项进行因式分解:
(1).(x+2)(x+4)+1.
(2).x2﹣5x﹣6
(3).(a2+4)2﹣16a2
(4).18b(a﹣b)2﹣12(a﹣b)3
【答案】(1)(x+3)2(2)(x﹣6)(x+1);(3)(a+2)2(a﹣2)2;(4) 6(a﹣b)2(5b﹣2a)
【解析】试题分析:(1)先展开合并后利用完全平方公式因式分解即可;(2)利用十字相乘法因式分解即可;(3)先利用平方差公式,再利用完全平方公式分解因式即可;(4)直接利用提公因式法因式分解即可.
试题解析:
(1)原式=x2+6x+9=(x+3)2.
(2)原式=(x﹣6)(x+1);
(3)原式=(a2+4+4a)(a2+4﹣4a)=(a+2)2(a﹣2)2;
(4)原式=6(a﹣b)2(3b﹣2a+2b)=6(a﹣b)2(5b﹣2a);
【题型】解答题
【结束】
23
【题目】计算下列各分式:
(1). ![]()
(2). ![]() -a+b
-a+b
(3). ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,已知
中,已知![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点,点
的中点,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边上运动(点
边上运动(点![]() 不与点
不与点![]() 、
、![]() 重合),且保持
重合),且保持![]() ,连接
,连接![]() 、
、![]() 、
、![]() .在此运动变化的过程中,有下列结论,其中正确的结论是( )
.在此运动变化的过程中,有下列结论,其中正确的结论是( )
①四边形![]() 有可能成为正方形;②
有可能成为正方形;②![]() 是等腰直角三角形;
是等腰直角三角形;
③四边形![]() 的面积是定值;④点
的面积是定值;④点![]() 到线段
到线段![]() 的最大距离为
的最大距离为![]() .
.
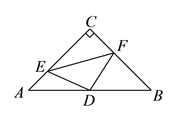
A. ①④ B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 过点(-2,5),和直线
过点(-2,5),和直线![]() ,分别在下列条件下求这个一次函数的解析式.
,分别在下列条件下求这个一次函数的解析式.
(1)它的图象与直线![]() 平行;
平行;
(2)它的图象与y轴的交点和直线![]() 与y轴的交点关于
与y轴的交点关于![]() 轴对称.
轴对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 为
为![]() 上的一点,按下列要求进行作图.
上的一点,按下列要求进行作图.
(1)作![]() 的平分线
的平分线![]() .
.
(2)在![]() 上取一点
上取一点![]() ,使得
,使得![]() .
.
(3)爱动脑筋的小刚经过仔细观察后,进行如下操作:在边![]() 上取一点
上取一点![]() ,使得
,使得![]() ,这时他发现
,这时他发现![]() 与
与![]() 之间存在一定的数量关系,请写出
之间存在一定的数量关系,请写出![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com