
 在正方形ABCO中,A(0,4),B(4,4),C(4,0),O(0,0),E为AO的中点,F为边CO上的动点,分别连接EF,FB,BE得到△EFB,并将其沿FB折叠得到△E′FB.
在正方形ABCO中,A(0,4),B(4,4),C(4,0),O(0,0),E为AO的中点,F为边CO上的动点,分别连接EF,FB,BE得到△EFB,并将其沿FB折叠得到△E′FB.分析 (1)根据勾股定理即可得到BE,EF的长,再根据折叠的性质知BE′=BE=2$\sqrt{5}$,FE′=EF=2$\sqrt{5}$,进而得到BE=EF=FE′=E′B,据此可得四边形BEFE′是菱形;
(2)先过E'作E'H⊥x轴于H,作E'G⊥y轴于G,连接EE',交BF于Q,根据勾股定理求得EE'的长,再设E'H=x,CH=y,则OG=x,GE'=4+y,根据勾股定理得出方程组,求得x和y的值,进而得到点E′的坐标.
解答 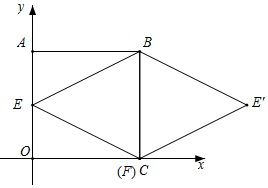 解:(1)四边形BEFE′是菱形,理由如下:
解:(1)四边形BEFE′是菱形,理由如下:
如图,∵E为AO的中点,
∴AE=EO=2,
∴BE=EF=$\sqrt{A{B}^{2}+A{E}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
由折叠的性质知BE′=BE=2$\sqrt{5}$,FE′=EF=2$\sqrt{5}$,
∴BE=EF=FE′=E′B,
∴四边形BEFE′是菱形;
(2)如图所示,过E'作E'H⊥x轴于H,作E'G⊥y轴于G,连接EE',交BF于Q,
∵E为AO的中点,F为CO的中点,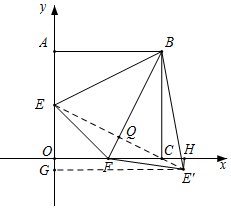
∴EF=$\sqrt{O{E}^{2}+O{F}^{2}}$=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,BE=BF=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
设FQ=a,则BQ=2$\sqrt{5}$-a,
∵EF2-FQ2=EB2-BQ2,
∴(2$\sqrt{2}$)2-a2=(2$\sqrt{5}$)2-(2$\sqrt{5}$-a)2,
解得a=$\frac{2}{5}\sqrt{5}$,
∴Rt△EFQ中,EQ=$\frac{6}{5}\sqrt{5}$,
由折叠可得,EE'=$\frac{12}{5}\sqrt{5}$,
由折叠的性质知FE′=EF=2$\sqrt{2}$,
设E'H=x,CH=y,则OG=x,GE'=4+y,
∵Rt△EE'G中,EG2+E'G2=EE'2,
∴(2+x)2+(4+y)2=($\frac{12}{5}\sqrt{5}$)2,①
∵Rt△FE'H中,FH2+E'H2=E'F2,
∴(2+y)2+x2=(2$\sqrt{2}$)2,②
由①和②解得$\left\{\begin{array}{l}{x=\frac{2}{5}}\\{y=\frac{4}{5}}\end{array}\right.$,(负值已舍去)
∴E'H=$\frac{2}{5}$,CH=$\frac{4}{5}$,
∴OH=4.8,E'H=0.4,
∴E'(4.8,-0.4).
点评 本题主要考查了折叠问题,菱形的判定以及勾股定理的运用,解决问题的关键是作辅助线构造直角三角形,依据勾股定理列方程求解,解题时注意:四条边相等的四边形是菱形;翻折变换(折叠问题)实质上就是轴对称变换.


科目:初中数学 来源: 题型:选择题
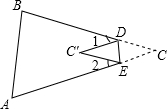 如图,将△ABC纸片的一角折叠,使点C落在△ABC内一点C′上,若∠1=30°,∠2=36°,则∠C的度数是( )
如图,将△ABC纸片的一角折叠,使点C落在△ABC内一点C′上,若∠1=30°,∠2=36°,则∠C的度数是( )| A. | 33° | B. | 34° | C. | 31° | D. | 32° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
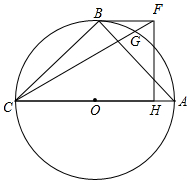 如图,△ABC内接于⊙O,AC是直径,BC=BA,在∠ACB的内部作∠ACF=30°,且CF=CA,过点F作FH⊥AC于点H,连接BF.
如图,△ABC内接于⊙O,AC是直径,BC=BA,在∠ACB的内部作∠ACF=30°,且CF=CA,过点F作FH⊥AC于点H,连接BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 若将三个数$\sqrt{3}$,3$\sqrt{2}$,2$\sqrt{3}$表示在数轴上,则能被如图所示的墨迹覆盖的数是$\sqrt{3}$.
若将三个数$\sqrt{3}$,3$\sqrt{2}$,2$\sqrt{3}$表示在数轴上,则能被如图所示的墨迹覆盖的数是$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠A=40°,∠C=70°,BD平分∠ABC,交AC于点D,则∠ABD的度数是( )
如图,在△ABC中,∠A=40°,∠C=70°,BD平分∠ABC,交AC于点D,则∠ABD的度数是( )| A. | 35° | B. | 40° | C. | 45° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
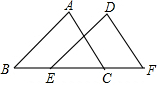 如图所示,△DEF是由△ABC经过平移得到的,则平移的距离可能是( )
如图所示,△DEF是由△ABC经过平移得到的,则平移的距离可能是( )| A. | 线段BC的长度 | B. | 线段EC的长度 | C. | 线段BE的长度 | D. | 线段BF的长度 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一组对边平行且相等,一个角是直角 | |
| B. | 对角线互相平分且相等 | |
| C. | 有三个角是直角 | |
| D. | 一组对边平行,另一组对边相等,且对角线相等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com