
 如图,已知点C为直线y=x上在第一象限内一点,直线y=2x+1交y轴于点A,交x轴于B,将直线AB沿射线OC方向平移$\sqrt{2}$个单位,则平移后直线的解析式为y=2x.
如图,已知点C为直线y=x上在第一象限内一点,直线y=2x+1交y轴于点A,交x轴于B,将直线AB沿射线OC方向平移$\sqrt{2}$个单位,则平移后直线的解析式为y=2x. 分析 设点A沿射线OC方向平移$\sqrt{2}$个单位后到达点M,点B沿射线OC方向平移$\sqrt{2}$个单位后到达点N,过点M作ME⊥y轴于点M,过点N作NF⊥x轴于点F,则△AEM和△BFN为等腰直角三角形,根据直线AB的解析式利用一次函数图象上点的坐标特征即可得出点A、B的坐标,根据等腰直角三角形的性质结合AM=BN=$\sqrt{2}$即可得出点M、N的坐标,再利用待定系数法即可求出平移后直线的解析式.
解答 解:设点A沿射线OC方向平移$\sqrt{2}$个单位后到达点M,点B沿射线OC方向平移$\sqrt{2}$个单位后到达点N,过点M作ME⊥y轴于点M,过点N作NF⊥x轴于点F,如图所示.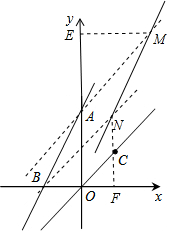
∵直线OC的解析式为y=x,
∴∠COF=∠COA=45°.
∵AM∥OC、BN∥OC,
∴∠NBF=∠COF=45°,∠MAE=∠COA=45°,
∴△AEM和△BFN为等腰直角三角形,且AM=BN=$\sqrt{2}$,
∴BF=NF=AE=EM=1.
当x=0时,y=2x+1=1,
∴点A的坐标为(0,1);
当y=2x+1=0时,x=-$\frac{1}{2}$,
∴点B的坐标为(-$\frac{1}{2}$,0).
∴点M的坐标为(1,2),点N的坐标为($\frac{1}{2}$,1).
设直线MN的解析式为y=kx+b,
将M(1,2)、N($\frac{1}{2}$,1)代入y=kx+b,
$\left\{\begin{array}{l}{k+b=2}\\{\frac{1}{2}k+b=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=2}\\{b=0}\end{array}\right.$,
∴直线MN的解析式为y=2x.
故答案为:y=2x.
点评 本题考查了一次函数图象与几何变换、等腰直角三角形的判定与性质、一次函数图象上点的坐标特征以及待定系数法求一次函数解析式,根据平移的特征找出点A、B平移后的坐标是解题的关键.


科目:初中数学 来源: 题型:选择题
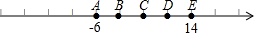 如图,A、B、C、D、E是未标出原点的数轴上的五个点,点A和点E对应的数位-6和14,且AB=BC=CD=DE,则点D所表示的数是( )
如图,A、B、C、D、E是未标出原点的数轴上的五个点,点A和点E对应的数位-6和14,且AB=BC=CD=DE,则点D所表示的数是( )| A. | 12 | B. | 9 | C. | 6 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
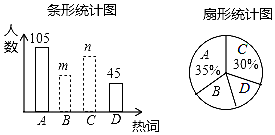 2016年《政府工作报告》中提出了十大新词汇,为了解同学们对新词汇的关注度,某数学兴趣小组选取其中的A:“互联网+政务服务”,B:“工匠精神”,C:“光网城市”,D:“大众旅游时代”四个热词在全校学生中进行了抽样调查,要求被调查的每位同学只能从中选择一个我最关注的热词、根据调查结果,该小组绘制了两幅不完整的统计图如图所示,请你根据统计图提供的信息,解答下列问题:
2016年《政府工作报告》中提出了十大新词汇,为了解同学们对新词汇的关注度,某数学兴趣小组选取其中的A:“互联网+政务服务”,B:“工匠精神”,C:“光网城市”,D:“大众旅游时代”四个热词在全校学生中进行了抽样调查,要求被调查的每位同学只能从中选择一个我最关注的热词、根据调查结果,该小组绘制了两幅不完整的统计图如图所示,请你根据统计图提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
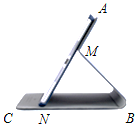 如图为一种平板电脑保护套的支架侧视图,AM固定于平板电脑背面,与可活动的MB、CB部分组成支架,为了观看舒适,可以调整倾斜角∠ANB的大小,但平板的下端点N只能在底座边CB上.不考虑拐角处的弧度及平板电脑和保护套的厚度,绘制成图(见答题纸),其中AN表示平板电脑,M为AN上的定点,AN=CB=20 cm,AM=8 cm,MB=MN,根据以上数据,判断倾斜角∠ANB能小于30°吗?请说明理由.
如图为一种平板电脑保护套的支架侧视图,AM固定于平板电脑背面,与可活动的MB、CB部分组成支架,为了观看舒适,可以调整倾斜角∠ANB的大小,但平板的下端点N只能在底座边CB上.不考虑拐角处的弧度及平板电脑和保护套的厚度,绘制成图(见答题纸),其中AN表示平板电脑,M为AN上的定点,AN=CB=20 cm,AM=8 cm,MB=MN,根据以上数据,判断倾斜角∠ANB能小于30°吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
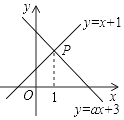 如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组$\left\{\begin{array}{l}{x-y=-1}\\{ax-y=-3}\end{array}\right.$的解是( )
如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组$\left\{\begin{array}{l}{x-y=-1}\\{ax-y=-3}\end{array}\right.$的解是( )| A. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将一直角三角板与两边平行的纸条如图所示放置,下列结论:①∠1=∠2 ②∠3=∠4 ③∠4+∠5=180° ④∠2+∠3=90°
如图,将一直角三角板与两边平行的纸条如图所示放置,下列结论:①∠1=∠2 ②∠3=∠4 ③∠4+∠5=180° ④∠2+∠3=90°| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com