
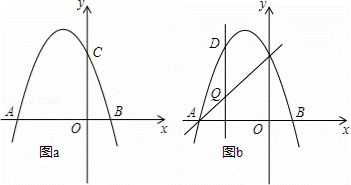
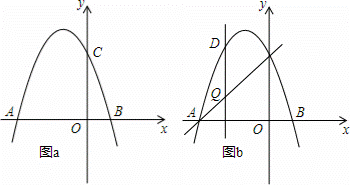
如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4SBOC,求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
解:(1)把A(﹣3,0),C(0,3)代入y=﹣x2+bx+c,得
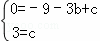 ,
,
解得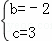 .
.
故该抛物线的解析式为:y=﹣x2﹣2x+3.
(2)由(1)知,该抛物线的解析式为y=﹣x2﹣2x+3,则易得B(1,0).
∵S△AOP=4S△BOC,
∴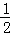 ×3×|﹣x2﹣2x+3|=4×
×3×|﹣x2﹣2x+3|=4×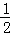 ×1×3.
×1×3.
整理,得(x+1)2=0或x2+2x﹣7=0,
解得x=﹣1或x=﹣1± .
.
则符合条件的点P的坐标为:(﹣1,4)或(﹣1+ ,﹣4)或(﹣1﹣
,﹣4)或(﹣1﹣ ,﹣4);
,﹣4);
(3)设直线AC的解析式为y=kx+t,将A(﹣3,0),C(0,3)代入,
得 ,
,
解得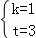 .
.
即直线AC的解析式为y=x+3.
设Q点坐标为(x,x+3),(﹣3≤x≤0),则D点坐标为(x,﹣x2﹣2x+3),
QD=(﹣x2﹣2x+3)﹣(x+3)=﹣x2﹣3x=﹣(x+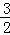 )2+
)2+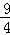 ,
,
∴当x=﹣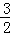 时,QD有最大值
时,QD有最大值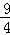 .
.


科目:初中数学 来源: 题型:
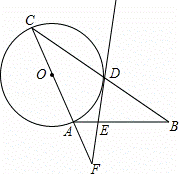
如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
(1)求证:FE⊥AB;
(2)当EF=6, =
=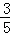 时,求DE的长.
时,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙两人在操场上赛跑,他们赛跑的路程S(米)与时间t(分钟)之间的函数关系如图所示,则下列说法错误的是( )
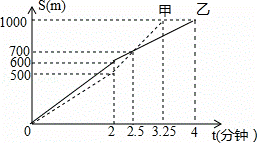
A. 甲、乙两人进行1000米赛跑
B. 甲先慢后快,乙先快后慢
C. 比赛到2分钟时,甲、乙两人跑过的路程相等
D. 甲先到达终点
查看答案和解析>>
科目:初中数学 来源: 题型:
小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍.小颖在小亮出发后50min 才乘上缆车,缆车的平均速度为180m/min.设小亮出发x min后行走的路程为y m,图中的折线表示小亮在整个行走过程中y与x的函数关系.
(1)小亮行走的总路程是 m,他途中休息了 min;
(2)①当50≤x≤80时,求y与x的函数关系式;
②当小颖到达缆车终点时,小亮离缆车终点的路程是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com