
����Ŀ����ͼ����һ��������ԭ��O�͵�B������һ�£��õ�һ����������������ͼ�е�A��ʾ��11����B��ʾ10����C��ʾ18�����dzƵ�A�͵�C�����������29�����ȵ�λ������P�ӵ�A��������2��λ/����ٶ��������������������������˶����ӵ�O�˶�����B�ڼ��ٶȱ�Ϊԭ����һ�룬֮�����ָ̻�ԭ�٣�ͬʱ������Q�ӵ�C��������1��λ/����ٶ���������ĸ������˶����ӵ�B�˶�����O�ڼ��ٶȱ�Ϊԭ����������֮��Ҳ���ָ̻�ԭ�٣����˶���ʱ��Ϊt�룮
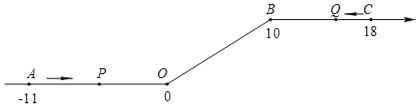
�ʣ���1������P�ӵ�A�˶���C����Ҫ����ʱ�䣿
��2��P��Q��������ʱ�����������M����Ӧ�����Ƕ��٣�
��3����tΪ��ֵʱ��P��O���������������ij�����Q��B���������������ij�����ȣ�
���𰸡���1������P�ӵ�A�˶���C����Ҫ19.5ʱ�䣻��2��M����Ӧ����Ϊ5����3��t��ֵΪ3��6.75��10.5��18��
�������������������1������·�̳����ٶȵ���ʱ�䣬�ֱ����������õ�ʱ�䣬��Ӽ��ɵô𰸣� ��2�������֪��P��Q�����������߶�OB����M������OM=x����������ʱP��Q�˶����õ�ʱ����ȣ��г����̣��ⷽ�̼��ɵô𰸣���3������PO��BQ��ʱ����ȣ��ɵ÷��̣����ݽⷽ�̣��ɵô𰸣���3��P��O���������������ij�����Q��B���������������ij��������4�ֿ��ܣ��ٶ���Q��CB�ϣ�����P��AO�ϣ��ڶ���Q��CB�ϣ�����P��OB�ϣ��۶���Q��BO�ϣ�����P��OB�ϣ��ܶ���Q��OA�ϣ�����P��BC�ϣ���������������ֱ��г����̣��ⷽ����tֵ����.
���������
��1����P�˶�����Cʱ������ʱ��t=11��2+10��1+8��2=19.5���룩��
�𣺶���P�ӵ�A�˶���C����Ҫ19.5ʱ�䣻
��2�������֪��P��Q�����������߶�OB����M������OM=x��
��11��2+x��1=8��1+��10��x����2��
x=5��
��M����Ӧ����Ϊ5��
��3��P��O���������������ij�����Q��B���������������ij��������4�ֿ��ܣ�
�ٶ���Q��CB�ϣ�����P��AO�ϣ�
��8��t=11��2t����ã�t=3��
�ڶ���Q��CB�ϣ�����P��OB�ϣ�
��8��t=��t��5.5����1����ã�t=6.75��
�۶���Q��BO�ϣ�����P��OB�ϣ�
��2��t��8��=��t��5.5����1����ã�t=10.5��
�ܶ���Q��OA�ϣ�����P��BC�ϣ�
��10+2��t��15.5��=t��13+10����ã�t=18��
����������t��ֵΪ3��6.75��10.5��18��


 ��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д� �����������Ż�ѧϰϵ�д�
�����������Ż�ѧϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x�ķ���ax2+3x��ax+2��һԪ���η��̣���ô��������
A.a��0B.a��1C.a��2D.a��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB=3cm��AD=9cm�����˳������۵���ʹ��B���D�غϣ��ۺ�ΪEF�����ABE������� 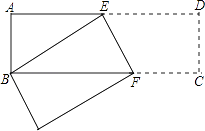
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��E��������ABCD�ı�DC��һ�㣬����A��FA=AE��CB���ӳ����ڵ�F����AB=4�����ı���AFCE������ǣ� �� 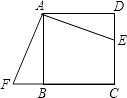
A.4
B.8
C.16
D.������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a>b����cΪ���������� ��
A. ac>bc B. ac<bc C. ac2>bc2 D. ac2��bc2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������ABC�͡�ADEΪ�ȱ������Σ�M��N�ֱ�EB��CD���е㣬��֤��CD=BE����AMN�ǵȱ������Σ�
(1)���ѡ�ADE��A����ת��ͼ2��λ��ʱ��CD=BE�Ƿ���Ȼ��������������֤��������������˵�����ɣ�
(2)����ADE��A����ת��ͼ3��λ��ʱ����AMN�Ƿ��ǵȱ������Σ����������֤����
(3)��(2)�������£������AB=2ADʱ����ADE���ABC����AMN�����֮��S��ADE��S��ABC�� S��AMN��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����6x��9��10x��45�뷽��3a��1��3��x��a����2a�Ľ���ͬ
��1���������ͬ�Ľ⣻
��2����a��ֵ��
��3����[m]��ʾ������m�������������[![]() ��2]��ֵ
��2]��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
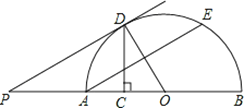
����Ŀ����ͼ��AB�ǰ�Բ��ֱ������O��Բ�ģ���C��OA���е㣬CD��OA����Բ�ڵ�D����E��![]() ���е㣬����AE��OD������D��DP��AE��BA���ӳ����ڵ�P��
���е㣬����AE��OD������D��DP��AE��BA���ӳ����ڵ�P��
��1�����AOD�Ķ�����
��2����֤��PD�ǰ�ԲO�����ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����괺��ǰϦ��������ѧ��ȫУ3000��ѧ�����������ٿ�����Ⱦ���ٷ��̻��������飬���ں������ȡ100��ѧ�������ʾ����飬�ʾ�ѡ�������A.�Լ�û��ȼ���̻�����B.�ڹ涨ʱ��涨�ص�����ȼ���̻�����C.����ȼ���̻�����D.�����Լ���ȼ��ͬʱȰ���������Ѳ�ȼ���̻�����.�������������Ƴ���������ͳ��ͼ�������������������ͼ�����ش��������⣺
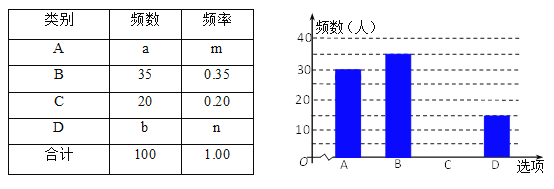
��1��������a= ��b= ������ȫ����ͳ��ͼ��
��2�������������ͳ��ͼ�������C����ռ��Բ�ĽǵĶ�����
��3�����ݳ�������������ȫУ���Լ�û��ȼ���̻����͡������Լ���ȼ��ͬʱȰ���������Ѳ�ȼ���̻�����ѧ�����ж�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com