练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知方程6x－9＝10x－45与方程3a－1＝3（x＋a）－2a的解相同

    （1）求这个相同的解；

    （2）求a的值；

    （3）若[m]表示不大于m的最大整数，求[－2]的值

    【答案】（1）x＝9；（2）a＝14；（3）2

    【解析】试题分析：（1）方程6x－9＝10x－45即可得出这个相同的解；（2）把（1）中的解代入方程3a－1＝3（x＋a）－2a，然后解以a为未知数的方程即可；（3）把a的值代入[－2]，根据[m]的定义求解即可．

    试题解析：（1）6x－9＝10x－45，6x-10x=9－45，-4x=-36，x=9；（2）把x=9代入方程3a－1＝3（x＋a）－2a得：3a－1＝3（9＋a）－2a，3a－1＝27＋3a－2a，2a=28，a＝14，（3）因为a＝14，所以[－2]= [－2]=[ ]=2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】飞机的无风飞行航速为a千米/时，风速为20千米/时．则飞机顺风飞行4小时的行程是千米；飞机逆风飞行3小时的行程是千米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在Rt△ABC中，各边都扩大5倍，则角A的三角函数值（　　）

    A. 不变B. 扩大5倍C. 缩小5倍D. 不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将一条数轴在原点O和点B处各折一下，得到一条“折线数轴”．图中点A表示﹣11，点B表示10，点C表示18，我们称点A和点C在数轴上相距29个长度单位．动点P从点A出发，以2单位/秒的速度沿着“折线数轴”的正方向运动，从点O运动到点B期间速度变为原来的一半，之后立刻恢复原速；同时，动点Q从点C出发，以1单位/秒的速度沿着数轴的负方向运动，从点B运动到点O期间速度变为原来的两倍，之后也立刻恢复原速．设运动的时间为t秒．

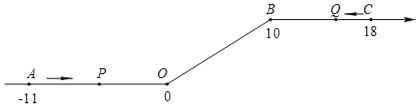
    问：（1）动点P从点A运动至C点需要多少时间？

    （2）P、Q两点相遇时，求出相遇点M所对应的数是多少；

    （3）求当t为何值时，P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动，甲点依顺时针方向环行，乙点依逆时针方向环行．若甲的速度是乙的速度的3倍，则它们第2018次相遇在___边上．

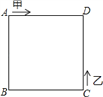
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线l上有AB两点，AB＝18cm，点O是线段AB上的一点，OA＝2OB

    （1）OA＝ cm ， OB＝ cm；

    （2）若点C是直线AB上一点，且满足AC＝CO+CB，求CO的长；

    （3）若动点P，Q分别从A，B同时出发，向右运动，点P的速度为2cm/s，点Q的速度为1cm/s．设运动时间为ts，当点P与点Q重合时，P，Q两点停止运动．

    ①当t为何值时，2OP﹣OQ＝3；

    ②当点P经过点O时，动点M从点O出发，以4cm/s的速度也向右运动．当点M追上点Q后立即返回，以4cm/s的速度向点P运动，遇到点P后再立即返回，以4cm/s的速度向点Q运动，如此往返.当点P与点Q重合时，P，Q两点停止运动．此时点M也停止运动．在此过程中，点M行驶的总路程是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“抢红包”是2015年春节十分火爆的一项网络活动，某企业有4000名职工，从中随机抽取350人，按年龄分布和“抢红包”所持态度情况进行调查，并将调查结果绘成了条形统计图和扇形统计图．

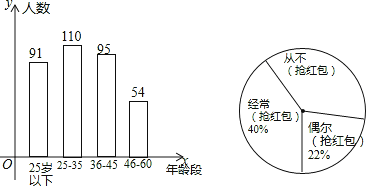
    （1）这次调查中，如果职工年龄的中位数是整数，那么这个中位数所在的年龄段是哪一段？

    （2）如果把对“抢红包”所持态度中的“经常（抢红包）”和“偶尔（抢红包）”统称为“参与抢红包”，那么这次接受调查的职工中“参与抢红包”的人数是多少？并估计该企业“从不（抢红包）”的人数是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某班要从9名百米跑成绩各不相同的同学中选4名参加4×100米接力赛，而这9名同学只知道自己的成绩，要想让他们知道自己是否入选,老师只需公布他们成绩的（　　）
    A.平均数
    B.中位数
    C.众数
    D.方差

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，OD，OE分别是∠AOC和∠BOC的平分线，∠AOD=40°，∠BOE=25°，求∠AOB的度数．

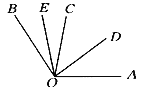
    解：∵OD平分∠AOC，OE平分∠BOC（已知），

    ∴∠AOC=2∠AOD，∠BOC=2________（ ），

    ∵∠AOD=40°，∠______=25°（已知），

    ∴∠AOC=2×40°=80°（等量代换），∠BOC=2×_____°=______°，

    ∴∠AOB=________°．

    查看答案和解析>>

    同步练习册答案