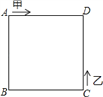
【题目】如图，甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动，甲点依顺时针方向环行，乙点依逆时针方向环行．若甲的速度是乙的速度的3倍，则它们第2018次相遇在___边上．
【答案】AD
【解析】设正方形的边长为a，因为甲的速度是乙的速度的3倍，时间相同，甲乙所行的路程比为3：1，由题意知：
①第一次相遇甲乙行的路程和为2a，甲行的路程为2a×
=
，乙行的路程为2a×
=
，在CD边相遇；
②第二次相遇甲乙行的路程和为4a，甲行的路程为4a×
=3a，乙行的路程为4a×
=a，在AD边相遇；
③第三次相遇甲乙行的路程和为4a，甲行的路程为4a×
=3a，乙行的路程为4a×
=a，在AB边相遇；
④第四次相遇甲乙行的路程和为4a，甲行的路程为4a×
=3a，乙行的路程为4a×
=a，在BC边相遇；
⑤第五次相遇甲乙行的路程和为4a，甲行的路程为4a×
=3a，乙行的路程为4a×
=a，在CD边相遇；
…
因为2018=504×4+2，所以它们第2018次相遇在边AD上．
故答案为：AD
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的B′处，若AE=2，DE=6，∠EFB=60°，则矩形ABCD的面积是（ ）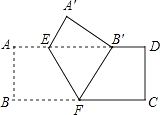
A.12
B.24
C.12 
D.16
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在矩形ABCD中，AD=2AB=4，E是AD的中点，一块足够大的三角板的直角顶点与点E重合，将三角板绕点E旋转，三角板的两直角边分别交AB，BC（或它们的延长线）于点M，N．
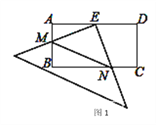
（1）观察图1，直接写出∠AEM与∠BNE的关系是 ；(不用证明)
（2）如图1，当M、N都分别在AB、BC上时，可探究出BN与AM的关系为： ；(不用证明)
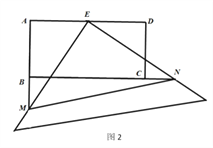
（3）如图2，当M、N都分别在AB、BC的延长线上时，（2）中BN与AM的关系式是否仍然成立？若成立，请说明理由：若不成立，写出你认为成立的结论，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】平面直角坐标系中，一个三角形的三个顶点的坐标，横坐标保持不变，纵坐标增加3个单位，则所得的图形与原图形相比（ ）．
A. 形状不变，大小扩大了3倍 B. 形状不变，向右平移了3个单位
C. 形状不变，向上平移了3个单位 D. 三角形被纵向拉伸为原来的3倍
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知方程6x－9＝10x－45与方程3a－1＝3（x＋a）－2a的解相同
（1）求这个相同的解；
（2）求a的值；
（3）若[m]表示不大于m的最大整数，求[
－2]的值
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB=AC，∠BAC=120°，AB的垂直平分线交BC于点D，那么∠DAC的度数为（ ）
A. 90° B. 80° C. 70° D. 60°
查看答案和解析>>
科目：初中数学 来源： 题型：
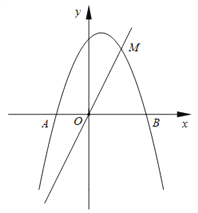
【题目】如图，在直角坐标系中，抛物线
与
轴交于
、
两点，与直线
交于点
．
(1)求
， 
的值；
(2)已知点
，点
关于原点
对称，现将线段
沿
轴向上平移
(
>0)个单位长度．若线段
与抛物线有两个不同的公共点，试求
的取值范围；
(3)利用尺规作图，在该抛物线上作出点
，使得
，并简要说明理由．(保留作图痕迹)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列几个算式：①a4·a4＝2a4；②x3＋x2＝x5；③a2·a3·a＝a5；④a4＋a4＝a8.其中计算正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com