
【题目】如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D,那么∠DAC的度数为( )

A. 90° B. 80° C. 70° D. 60°
科目:初中数学 来源: 题型:
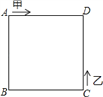
【题目】如图,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若甲的速度是乙的速度的3倍,则它们第2018次相遇在___边上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)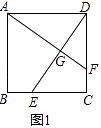
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;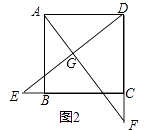
(3)如图3,在(2)的基础上,连接AE和EF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.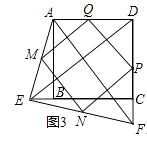
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“抢红包”是2015年春节十分火爆的一项网络活动,某企业有4000名职工,从中随机抽取350人,按年龄分布和“抢红包”所持态度情况进行调查,并将调查结果绘成了条形统计图和扇形统计图.
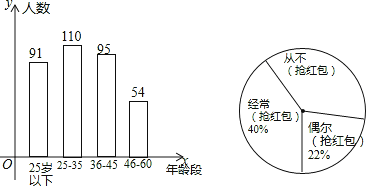
(1)这次调查中,如果职工年龄的中位数是整数,那么这个中位数所在的年龄段是哪一段?
(2)如果把对“抢红包”所持态度中的“经常(抢红包)”和“偶尔(抢红包)”统称为“参与抢红包”,那么这次接受调查的职工中“参与抢红包”的人数是多少?并估计该企业“从不(抢红包)”的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
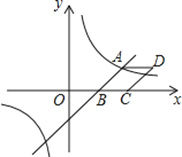
【题目】如图,已知一次函数y=![]() x-3与反比例函数
x-3与反比例函数![]() 的图象相交于点A
的图象相交于点A![]() ,与x轴相交于点B.
,与x轴相交于点B.
(1)填空: ![]() 的值为 ,
的值为 , ![]() 的值为 ;
的值为 ;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比函数![]() 的图象,当
的图象,当![]() 时,请直接写出自变量
时,请直接写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,D为BC边上一点,DE⊥AB于E,DF⊥AC于F.
作图:
(1)请作出AC边上的高BG.
探究:
(2)请你通过观察、测量找到DE、DF、BG之间的数量关系: ;
(3)为了说明DE、DF、BG之间的数量关系,小嘉是这样做的:
连接AD,则S△ADC= ,S△ABD= ,∴S△ABC= ,S△ABC还可以表示为 …
请你帮小嘉完成上述填空:
拓展:
(4)如图2,当D在如图2的位置时,上面DE、DF、BG之间的数量关系是否仍然成立?并说明理由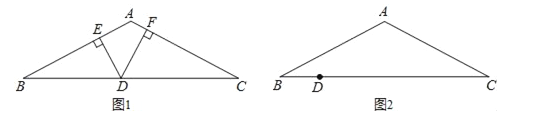
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com