
【题目】如图1,在△ABC中,AB=AC,D为BC边上一点,DE⊥AB于E,DF⊥AC于F.
作图:
(1)请作出AC边上的高BG.
探究:
(2)请你通过观察、测量找到DE、DF、BG之间的数量关系: ;
(3)为了说明DE、DF、BG之间的数量关系,小嘉是这样做的:
连接AD,则S△ADC= ,S△ABD= ,∴S△ABC= ,S△ABC还可以表示为 …
请你帮小嘉完成上述填空:
拓展:
(4)如图2,当D在如图2的位置时,上面DE、DF、BG之间的数量关系是否仍然成立?并说明理由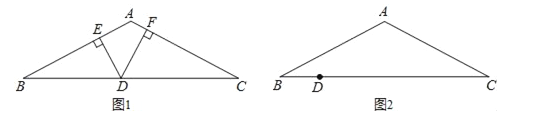
【答案】(1)答案见解析;(2)BG=DE+DF;(3)答案见解析;(4)成立.
【解析】试题分析:(1)按要求作出AC边上的高BG即可;
(2)连接AD,分别求出△ABD、△ADC与△ABC的面积,进而可得出结论;
(3)根据(2)中的过程即可得;
(4)根据(2)中的证明过程可得出结论.
试题解析:(1)如图所示:
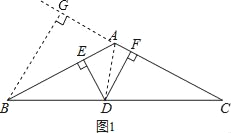
(2)BG=DE+DF,
连接AD,
∵DE⊥AB于E,DF⊥AC于F,AB=AC,
∴S△ABC=S△ABD+S△ACD=![]() ABDE+
ABDE+![]() ACDF=
ACDF=![]() AC(DE+DF),
AC(DE+DF),
∵BG⊥AC,
∴S△ABC=![]() ACBG,
ACBG,
∴BG=DE+DF,
故答案为:BG=DE+DF;
(3)由(2)可知,S△ADC=![]() ACDF,S△ABD=
ACDF,S△ABD=![]() ABDE,
ABDE,
∴S△ABC=![]() ACDF+
ACDF+![]() ABDE,
ABDE,
S△ABC还可以表示为![]() ACBG,
ACBG,
故答案为: ![]() ACDF,
ACDF, ![]() ABDE,
ABDE, ![]() ACDF+
ACDF+![]() ABDE,
ABDE, ![]() ACBG;
ACBG;
(4)拓展结论仍然成立,即BG=DE+DF,
连接AD,
∵DE⊥AB于E,DF⊥AC于F,AB=AC,
∴S△ABC=S△ABD+S△ACD=![]() ABDE+
ABDE+![]() ACDF=
ACDF=![]() AC(DE+DF),
AC(DE+DF),
∵BG⊥AC,
∴S△ABC=![]() ACBG,
ACBG,
∴BG=DE+DF.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AD=2AB=4,E是AD的中点,一块足够大的三角板的直角顶点与点E重合,将三角板绕点E旋转,三角板的两直角边分别交AB,BC(或它们的延长线)于点M,N.
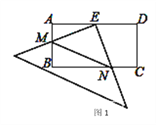
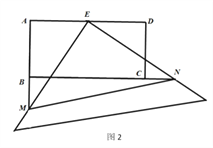
(1)观察图1,直接写出∠AEM与∠BNE的关系是 ;(不用证明)
(2)如图1,当M、N都分别在AB、BC上时,可探究出BN与AM的关系为: ;(不用证明)
(3)如图2,当M、N都分别在AB、BC的延长线上时,(2)中BN与AM的关系式是否仍然成立?若成立,请说明理由:若不成立,写出你认为成立的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D,那么∠DAC的度数为( )

A. 90° B. 80° C. 70° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() .
.
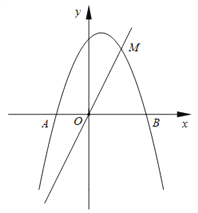
(1)求![]() ,
, ![]() 的值;
的值;
(2)已知点![]() ,点
,点![]() 关于原点
关于原点![]() 对称,现将线段
对称,现将线段![]() 沿
沿![]() 轴向上平移
轴向上平移![]() (
(![]() >0)个单位长度.若线段
>0)个单位长度.若线段![]() 与抛物线有两个不同的公共点,试求
与抛物线有两个不同的公共点,试求![]() 的取值范围;
的取值范围;
(3)利用尺规作图,在该抛物线上作出点![]() ,使得
,使得![]() ,并简要说明理由.(保留作图痕迹)
,并简要说明理由.(保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DE,则∠CDF等于( ) 
A.60°
B.65°
C.70°
D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为4cm,A为线段OP的中点,当OP=6cm时,点A与⊙O的位置关系是( )
A.A在⊙O内B.A在⊙O上C.A在⊙O外D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列几个算式:①a4·a4=2a4;②x3+x2=x5;③a2·a3·a=a5;④a4+a4=a8.其中计算正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
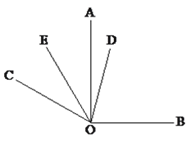
【题目】如图,已知同一平面内∠AOB=90°,∠AOC=60°.
(1)填空:∠BOC=__________;
(2)如果OD平分∠BOC,OE平分∠AOC,直接写出∠DOE的度数为_______;
(3)在(2)的条件下,将题目中∠AOC=60°改成∠AOC=![]() ,其它条件不变,请求出∠DOE的度数.
,其它条件不变,请求出∠DOE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com