
【题目】如图,在直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() .
.
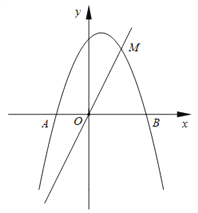
(1)求![]() ,
, ![]() 的值;
的值;
(2)已知点![]() ,点
,点![]() 关于原点
关于原点![]() 对称,现将线段
对称,现将线段![]() 沿
沿![]() 轴向上平移
轴向上平移![]() (
(![]() >0)个单位长度.若线段
>0)个单位长度.若线段![]() 与抛物线有两个不同的公共点,试求
与抛物线有两个不同的公共点,试求![]() 的取值范围;
的取值范围;
(3)利用尺规作图,在该抛物线上作出点![]() ,使得
,使得![]() ,并简要说明理由.(保留作图痕迹)
,并简要说明理由.(保留作图痕迹)
【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]() 取值范围为
取值范围为![]() ;(3)作图见解析,理由见解析.
;(3)作图见解析,理由见解析.
【解析】试题分析:(1)、根据一次函数解析求出点M的坐标,然后将点M的坐标代入二次函数解析式得出b的值;(2)、根据对称得出点N的坐标,过点N作CN⊥x轴,交抛物线于C,从而得出CN=AN=2,即当S=2时线段MN与抛物线有两个交点,然后设平移后的解析式为y=2x+s,然后将一次函数和二次函数联立成方程组,根据根的判别式得出s的值,从而得出取值范围;(3)、如图,在x轴上取一点P(-2,0)以P为圆心,OP为半径作圆,⊙P与抛物线的交点,即是所求作的点G,根据△GPA和△BPG相似得出答案.
试题解析:(1)、把![]() 代入
代入![]() 得
得![]()
把![]() 代入
代入![]() 得
得![]() 即
即![]()
(2)、由(1)得![]()
![]()
因为点![]() ,点
,点![]() 关于原点
关于原点![]() 对称,所以
对称,所以![]()
过点N作![]() 轴,交抛物线于C, 则C的横坐标为
轴,交抛物线于C, 则C的横坐标为![]()
所以C的纵坐标为![]() 所以
所以![]() 与
与![]() 重合.
重合.
则![]() ,即当
,即当![]() 线段
线段![]() 与抛物线有两个公共点
与抛物线有两个公共点
设平移后的直线表达式为![]() 由
由![]() 得
得![]()
由![]() 得
得![]() 即当
即当![]() 线段
线段![]() 与抛物线只有一个公共点.
与抛物线只有一个公共点.
所以,当线段![]() 与抛物线有两个公共点时.
与抛物线有两个公共点时. ![]() 取值范围为
取值范围为![]()
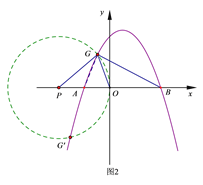
(3)、如图,在![]() 轴上取一点
轴上取一点![]() 以
以![]() 为圆心,
为圆心, ![]() 为半径作圆,⊙
为半径作圆,⊙![]() 与抛物线的交点,即是所求作的点
与抛物线的交点,即是所求作的点![]() (图中的
(图中的![]() 与
与![]() )
)
理由:当点![]() 在
在![]() 轴上方时, 由作图可知,
轴上方时, 由作图可知, ![]()
则![]() 又∵
又∵![]() ∴
∴![]() ∴
∴![]()
∵![]() ∴
∴![]()
又![]()
![]() ∴
∴![]()
同理可证:当点![]() (
(![]() )在
)在![]() 轴下方时,结论也成立.
轴下方时,结论也成立.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:初中数学 来源: 题型:
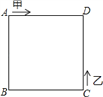
【题目】如图,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若甲的速度是乙的速度的3倍,则它们第2018次相遇在___边上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“抢红包”是2015年春节十分火爆的一项网络活动,某企业有4000名职工,从中随机抽取350人,按年龄分布和“抢红包”所持态度情况进行调查,并将调查结果绘成了条形统计图和扇形统计图.
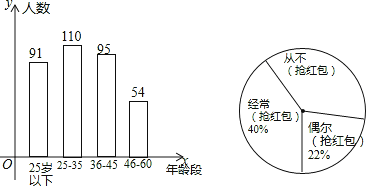
(1)这次调查中,如果职工年龄的中位数是整数,那么这个中位数所在的年龄段是哪一段?
(2)如果把对“抢红包”所持态度中的“经常(抢红包)”和“偶尔(抢红包)”统称为“参与抢红包”,那么这次接受调查的职工中“参与抢红包”的人数是多少?并估计该企业“从不(抢红包)”的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
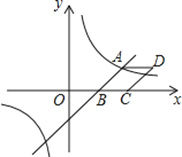
【题目】如图,已知一次函数y=![]() x-3与反比例函数
x-3与反比例函数![]() 的图象相交于点A
的图象相交于点A![]() ,与x轴相交于点B.
,与x轴相交于点B.
(1)填空: ![]() 的值为 ,
的值为 , ![]() 的值为 ;
的值为 ;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比函数![]() 的图象,当
的图象,当![]() 时,请直接写出自变量
时,请直接写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班要从9名百米跑成绩各不相同的同学中选4名参加4×100米接力赛,而这9名同学只知道自己的成绩,要想让他们知道自己是否入选,老师只需公布他们成绩的( )
A.平均数
B.中位数
C.众数
D.方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,D为BC边上一点,DE⊥AB于E,DF⊥AC于F.
作图:
(1)请作出AC边上的高BG.
探究:
(2)请你通过观察、测量找到DE、DF、BG之间的数量关系: ;
(3)为了说明DE、DF、BG之间的数量关系,小嘉是这样做的:
连接AD,则S△ADC= ,S△ABD= ,∴S△ABC= ,S△ABC还可以表示为 …
请你帮小嘉完成上述填空:
拓展:
(4)如图2,当D在如图2的位置时,上面DE、DF、BG之间的数量关系是否仍然成立?并说明理由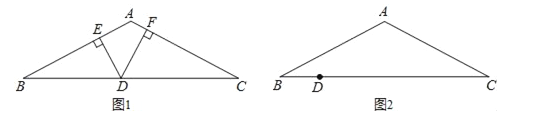
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一棵树CD的10m高处的B点有两只猴子,它们都要到A处池塘边喝水,其中一只猴子沿树爬下走到离树20m处的池塘A处,另一只猴子爬到树顶D后直线跃入池塘的A处.如果两只猴子所经过的路程相等,试问这棵树多高? 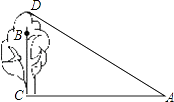
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com