
【题目】如图,直线l上有AB两点,AB=18cm,点O是线段AB上的一点,OA=2OB
![]()
(1)OA= cm , OB= cm;
(2)若点C是直线AB上一点,且满足AC=CO+CB,求CO的长;
(3)若动点P,Q分别从A,B同时出发,向右运动,点P的速度为2cm/s,点Q的速度为1cm/s.设运动时间为ts,当点P与点Q重合时,P,Q两点停止运动.
①当t为何值时,2OP﹣OQ=3;
②当点P经过点O时,动点M从点O出发,以4cm/s的速度也向右运动.当点M追上点Q后立即返回,以4cm/s的速度向点P运动,遇到点P后再立即返回,以4cm/s的速度向点Q运动,如此往返.当点P与点Q重合时,P,Q两点停止运动.此时点M也停止运动.在此过程中,点M行驶的总路程是多少?
【答案】(1)12,6;(2)CO的长为2或18cm;(3)①当t为3s或11s时,2OP﹣OQ=3;② 48cm.
【解析】试题分析: (1)由OA=2OB结合AB=OA+OB=18即可求出OA、OB的长度;
(2)设CO的长是xcm,分点C在线段AO上、在线段OB上以及在线段AB的延长线上三种情况考虑,根据两点间的距离公式结合AC=CO+CB即可得出关于x的一元一次方程,解之即可得出结论;
(3)找出运动时间为ts时,点P、Q表示的数,由点P、Q表示的数相等即可找出t的取值范围.
①由两点间的距离公式结合2OP-OQ=4即可得出关于t的含绝对值符号的一元一次方程,解之即可得出结论;
②令点P表示的数为0即可找出此时t的值,再根据路程=速度×时间即可算出点M行驶的总路程.
试题解析:
解:(1)∵AB=18cm,OA=2OB,
∴OA+OB=3OB=AB=18cm,
解得OB=6cm,
OA=2OB=12cm.
故答案为:12,6;
(2)设CO的长是xcm,依题意有
①当点C在线段AB上时12﹣x=x+6+x,
解得x=2.
②当点C在线段AB的延长线上时12+x=x+x-6
解得x=18
故CO的长为2或18cm;
(3)①当0≤t<4时,依题意有2(12﹣3t)﹣(6+t)=4,
解得t=2;
当4≤t<6时,依题意有2(3t﹣12)﹣(6+t)=4,
解得t=![]() 或t=6.8(不合题意舍去);
或t=6.8(不合题意舍去);
当6≤t≤9时,依题意有2(3t﹣12)﹣(6+t)=4,
解得t=![]() 或t=6.8
或t=6.8
故当t为2s或6.8s时,2OP﹣OQ=4;
②当3t12=0时,t=4,
4×(94)=20(cm).
答:在此过程中,点M行驶的总路程是20cm.
点睛: 本题考查了数轴及数轴的三要素(正方向、原点和单位长度).一元一次方程的应用以及数轴上两点之间的距离公式的运用,行程问题中的路程=速度×时间的运用.注意(3)①需要分类讨论.


科目:初中数学 来源: 题型:
【题目】在期中考试中,同学甲、乙、丙、丁分别获得第一、第二、第三、第四名.在期末考试中,他们又是班上的前四名.如果他们当中只有一位的排名与期中考试中的排名相同,那么排名情况有( )种可能.
A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( ) 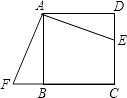
A.4
B.8
C.16
D.无法计算
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,若△ABC和△ADE为等边三角形,M,N分别EB,CD的中点,易证:CD=BE,△AMN是等边三角形.
(1)当把△ADE绕A点旋转到图2的位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由;
(2)当△ADE绕A点旋转到图3的位置时,△AMN是否还是等边三角形?若是请给出证明,
(3)在(2)的条件下,求出当AB=2AD时,△ADE与△ABC及△AMN的面积之比S△ADE∶S△ABC∶ S△AMN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知方程6x-9=10x-45与方程3a-1=3(x+a)-2a的解相同
(1)求这个相同的解;
(2)求a的值;
(3)若[m]表示不大于m的最大整数,求[![]() -2]的值
-2]的值
查看答案和解析>>
科目:初中数学 来源: 题型:
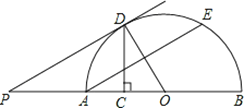
【题目】如图,AB是半圆的直径,点O是圆心,点C是OA的中点,CD⊥OA交半圆于点D,点E是![]() 的中点,连接AE、OD,过点D作DP∥AE交BA的延长线于点P.
的中点,连接AE、OD,过点D作DP∥AE交BA的延长线于点P.
(1)求∠AOD的度数;
(2)求证:PD是半圆O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校在“校园读书节”活动中,购买甲、乙两种图书共100本作为奖品,已知乙种图书的单价比甲种图书的单价高出50%.同样用360元购买乙种图书比购买甲种图书少4本.
(1)求甲、乙两种图书的单价各是多少元;
(2)如果购买图书的总费用不超过3500元,那么乙种图书最多能买多少本?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com