
����Ŀ����ͼ1������ABC�͡�ADEΪ�ȱ������Σ�M��N�ֱ�EB��CD���е㣬��֤��CD=BE����AMN�ǵȱ������Σ�
(1)���ѡ�ADE��A����ת��ͼ2��λ��ʱ��CD=BE�Ƿ���Ȼ��������������֤��������������˵�����ɣ�
(2)����ADE��A����ת��ͼ3��λ��ʱ����AMN�Ƿ��ǵȱ������Σ����������֤����
(3)��(2)�������£������AB=2ADʱ����ADE���ABC����AMN�����֮��S��ADE��S��ABC�� S��AMN��

���𰸡���1��(1)CD=BE�����ɼ���������2����AMN�ǵȱ������Σ����ɼ���������3��4:16:7
�������������������1����������SAS�ж���ABE�ա�ACD��Ȼ�����ȫ�������εĶ�Ӧ����ȣ��õ�CD=BE����2������֤����AMN�ǵȱ������Σ�AD=a����AB=2a����AB=2a����3��������֪�����ֱ������AMN�ı߳�����Ϊ��ADE����ABC����AMNΪ�ȱ������Σ���������ȵ��ڱ߳���ƽ���ıȣ��ݴ˽�ɣ�
(1)CD=BE���������£���
�ߡ�ABC����ADEΪ�ȱ������Σ�
��AB=AC��AE=AD����BAC=��EAD=60o��
�ߡ�BAE =��BAC����EAC =60o����EAC��
��DAC =��DAE����EAC =60o����EAC��
���BAE=��DAC��
���ABE �� ��ACD��
��CD=BE��
(2)��AMN�ǵȱ������Σ��������£�
�ߡ�ABE �� ��ACD��
���ABE=��ACD��
��M��N�ֱ���BE��CD���е㣬
��BM= ![]() ��
��
��AB=AC����ABE=��ACD��
���ABM �� ��ACN��
��AM=AN����MAB=��NAC��
���NAM=��NAC+��CAM=��MAB+��CAM=��BAC=60o��
���AMN�ǵȱ������Σ�
(3) ��AD=a����AB=2a��
��AD=AE=DE��AB=AC��
��CE=DE��
�ߡ�ADEΪ�ȱ������Σ�
���DEC=120 o�� ��ADE=60o��
���EDC=��ECD=30o��
���ADC=90o.
����Rt��ADC��AD=a����ACD=30 o ��
�� CD= ![]() ��
��
��NΪDC�е㣬
��![]() ��
��
�� ��
��
�ߡ�ADE����ABC����AMNΪ�ȱ������Σ�
��S��ADE��S��ABC�� S��AMN=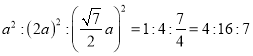


 �����������Ż�ѧϰϵ�д�
�����������Ż�ѧϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��23��17������7��+����16����
��2��-5+6�£�-2����![]() ��
��
��3��-36��![]() ��
��
��4����23+|5��8|+24�£���3����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ֶ������㡰�����������ʵ��a��b������a��b��a2��3a+b���磺3��5��32��3��3+5����x��2��6������ʵ��x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ϊ����һ��ɽ��CF�ĸ߶ȣ�����ɽ��ij��ɽ�»���ΪAB��BC���Σ�ÿһ��ɽ�½�������ֱ���ģ����в���³�AB=600�ף�BC=200�ף��½ǡ�BAF=30������CBE=45������ɽ��ĸ߶�CF������������ţ�
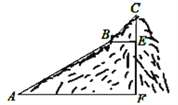
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ��������ԭ��O�͵�B������һ�£��õ�һ����������������ͼ�е�A��ʾ��11����B��ʾ10����C��ʾ18�����dzƵ�A�͵�C�����������29�����ȵ�λ������P�ӵ�A��������2��λ/����ٶ��������������������������˶����ӵ�O�˶�����B�ڼ��ٶȱ�Ϊԭ����һ�룬֮�����ָ̻�ԭ�٣�ͬʱ������Q�ӵ�C��������1��λ/����ٶ���������ĸ������˶����ӵ�B�˶�����O�ڼ��ٶȱ�Ϊԭ����������֮��Ҳ���ָ̻�ԭ�٣����˶���ʱ��Ϊt�룮
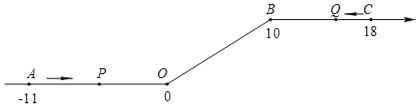
�ʣ���1������P�ӵ�A�˶���C����Ҫ����ʱ�䣿
��2��P��Q��������ʱ�����������M����Ӧ�����Ƕ��٣�
��3����tΪ��ֵʱ��P��O���������������ij�����Q��B���������������ij�����ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �ĶԳ���Ϊ
�ĶԳ���Ϊ![]() �ᣬ�Ҿ���(0��0)��(
�ᣬ�Ҿ���(0��0)��(![]() )���㣬��P�����������˶�����PΪԲ�ĵġ�P��������A(0��2)��
)���㣬��P�����������˶�����PΪԲ�ĵġ�P��������A(0��2)��
(1)��![]() ��ֵ��
��ֵ��
(2)��֤����P���˶������У���Pʼ����![]() ���ཻ��
���ཻ��
(3)���P��![]() ���ཻ��M
���ཻ��M![]() ��N
��N ![]() (
(![]() ��
��![]() )���㣬����AMNΪ����������ʱ����Բ��P�������꣮
)���㣬����AMNΪ����������ʱ����Բ��P�������꣮
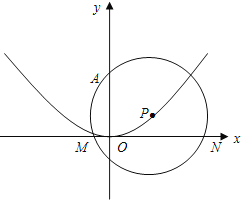
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l����AB���㣬AB��18cm����O���߶�AB�ϵ�һ�㣬OA��2OB
![]()
��1��OA�� cm �� OB�� cm��
��2������C��ֱ��AB��һ�㣬������AC��CO+CB����CO�ij���
��3��������P��Q�ֱ��A��Bͬʱ�����������˶�����P���ٶ�Ϊ2cm/s����Q���ٶ�Ϊ1cm/s�����˶�ʱ��Ϊts������P���Q�غ�ʱ��P��Q����ֹͣ�˶���
�ٵ�tΪ��ֵʱ��2OP��OQ��3��
�ڵ���P������Oʱ������M�ӵ�O��������4cm/s���ٶ�Ҳ�����˶�������M�ϵ�Q���������أ���4cm/s���ٶ����P�˶���������P�����������أ���4cm/s���ٶ����Q�˶����������.����P���Q�غ�ʱ��P��Q����ֹͣ�˶�����ʱ��MҲֹͣ�˶����ڴ˹����У���M��ʻ����·���Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������
��1������1��2014+����![]() ����2 ����3.14������0��
����2 ����3.14������0��
��2����2a+3b����2a��3b��+��3b��a��2��
��3���Ȼ�������ֵ��x��x+y������x+y��2+2xy������x=![]() ��y=��25��
��y=��25��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������ʽA��ȥ����ʽ2x2+5x��3��ijͬѧ�����ų����˼Ӻţ�������Ϊ��x2+3x��5����ô��ȷ���������ǣ� ��
A.��3x2��2x��4
B.��x2+3x��7
C.��5x2��7x+1
D.��ȷ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com