
如图,在?ABCD中,E是AD上一点,连接BE,F为BE中点,且AF=BF,

(1)求证:四边形ABCD为矩形;
(2)过点F作FG⊥BE,垂足为F,交BC于点G,若BE=BC,S△BFG=5,CD=4,求CG.
(1)证明见解析;(2)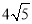 -5.
-5.
【解析】
试题分析:(1)求出∠BAE=90°,根据矩形的判定推出即可;
(2)求出△BGE面积,根据三角形面积公式求出BG,得出EG长度,根据勾股定理求出GH,求出BE,得出BC长度,即可求出答案.
试题解析:(1)证明:∵F为BE中点,AF=BF,
∴AF=BF=EF,
∴∠BAF=∠ABF,∠FAE=∠AEF,
在△ABE中,∠BAF+∠ABF+∠FAE+∠AEF=180°,
∴∠BAF+∠FAE=90°,
又四边形ABCD为平行四边形,
∴四边形ABCD为矩形;
(2)【解析】
连接EG,过点E作EH⊥BC,垂足为H,
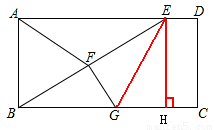
∵F为BE的中点,FG⊥BE,
∴BG=GE,
∵S△BFG=5,CD=4,
∴S△BGE=10=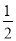 BG•EH,
BG•EH,
∴BG=GE=5,
在Rt△EGH中,GH=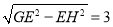
在Rt△BEH中,BE=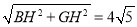 =BC,
=BC,
∴CG=BC-BG=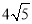 -5.
-5.
考点:1.矩形的判定与性质;2.勾股定理;3.平行四边形的性质.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2015届江苏省扬州市江都区八年级下学期期末考试数学试卷(解析版) 题型:填空题
在下列图形:①圆 ②等边三角形 ③矩形 ④平行四边形中,既是中心对称图形又是轴对称图形的是 (填写序号).
查看答案和解析>>
科目:初中数学 来源:2015届浙江省八年级上学期第二次月考数学试卷(解析版) 题型:解答题
(8分)△ABC在平面直角坐标系中的位置如图所示.

(1)作出与△ABC关于y轴对称的△A1B1C1;并写出所得像的各顶点坐标;
(2)将△ABC向下平移3个单位长度,画出平移后的△A2B2C2.并写出所得像的各顶点坐标。
查看答案和解析>>
科目:初中数学 来源:2015届湖北省武汉市黄陂区八年级下学期期末数学试卷(解析版) 题型:选择题
如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1,再以正方形的对角线OA2作正方形OA1A2B1,…,依此规律,则点A8的坐标是( )

A.(-8,0) B.(0,8) C.(0,8 ) D.(0,16)
) D.(0,16)
查看答案和解析>>
科目:初中数学 来源:2015届湖北省武汉市黄陂区八年级下学期期末数学试卷(解析版) 题型:解答题
在平面直角坐标系中,已知点A(a,0),C(0,b)满足(a+1)2+ =0
=0

(1)直接写出:a= -1,b= -3;
(2)点B为x轴正半轴上一点,如图1,BE⊥AC于点E,交y轴于点D,连接OE,若OE平分∠AEB,求直线BE的解析式;
(3)在(2)条件下,点M为直线BE上一动点,连OM,将线段OM逆时针旋转90°,如图2,点O的对应点为N,当点M的运动轨迹是一条直线l,请你求出这条直线l的解析式.
查看答案和解析>>
科目:初中数学 来源:2015届黑龙江省绥棱县八年级五四制上学期期末考试数学试卷(解析版) 题型:解答题
(本题9分)某中学新建了一栋四层的教学楼,每层楼有10间教室,进出这栋教学楼共有4个门,其中两个正门大小相同,两个侧门大小也相同.安全检查中,对4个门进行了测试,当同时开启一个正门和两个侧门时,2分钟内可以通过560名学生;当同时开启一个正门和一个侧门时,4分钟内可以通过800名学生.
(1)求平均每分钟开启一个正门和一个侧门各可以通过多少名学生?
(2)检查中发现,出现紧急情况时,因学生拥挤,出门的效率将降低20%,安全检查规定:在紧急情况下全楼的学生应在5分钟内通过这4个门安全撤离,假设这栋教学大楼每间教室最多有45名学生,问:该教学楼建造的这4个门是否符合安全规定?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com