
在平面直角坐标系中,已知点A(a,0),C(0,b)满足(a+1)2+ =0
=0

(1)直接写出:a= -1,b= -3;
(2)点B为x轴正半轴上一点,如图1,BE⊥AC于点E,交y轴于点D,连接OE,若OE平分∠AEB,求直线BE的解析式;
(3)在(2)条件下,点M为直线BE上一动点,连OM,将线段OM逆时针旋转90°,如图2,点O的对应点为N,当点M的运动轨迹是一条直线l,请你求出这条直线l的解析式.
(1) a=-1,b=-3.(2) 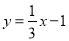 ;(3)
;(3) 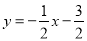 .
.
【解析】
试题分析:(1)根据非负数是性质来求a、b的值;
(2)如图1,过点O作OF⊥OE,交BE于F.构建全等三角形:△EOC≌△FOB(ASA),△AOC≌△DOB(ASA),易求D(0,-1),B(3,0).利用待定系数法求得直线BE的解析式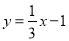 ;
;
(3)如图2,过点M作MG⊥x轴,垂足为G,过点N作NH⊥GH,垂足为H.构建全等三角形:△GOM≌△HMN,故OG=MH,GM=NH.设M(m,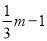 ),则H(m,
),则H(m,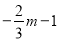 ),N(
),N(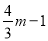 ,
,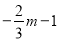 ),由此求得点N的横纵坐标间的函数关系.
),由此求得点N的横纵坐标间的函数关系.
试题解析:(1)依题意得 a+1=0,b+3=0,
解得 a=-1,b=-3.
(2)如图,过点O作OF⊥OE,交BE于F.
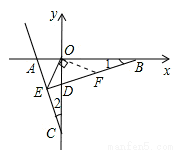
∵BE⊥AC,OE平分∠AEB,
∴△EOF为等腰直角三角形.
∵在△EOC与△FOB中,
 ,
,
∴△EOC≌△FOB(ASA),
∴OB=OC.
∴在△AOC与△DOB中,
 ,
,
∴△AOC≌△DOB(ASA),
∴OA=OD,
∵A(-1,0),B(0,-3),∴D(0,-1),B(3,0)
∴直线BD,即直线BE的解析式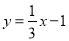 ;
;
(3)依题意,△NOM为等腰Rt△,
如图,过点M作MG⊥x轴,垂足为G,过点N作NH⊥GH,垂足为H,
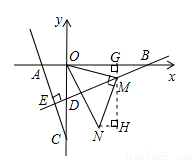
∵△NOM为等腰Rt△,
则易证△GOM≌△HMN,
∴OG=MH,GM=NH,
由(2)知直线BD的解析式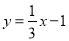
设M(m,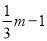 ),则H(m,
),则H(m,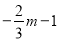 ),N(
),N(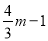 ,
,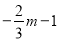 ),
),
令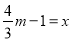 ,
, ,
,
消去参数m得,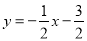
即直线l的解析式为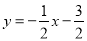 .
.
考点:一次函数综合题.


科目:初中数学 来源:2015届浙江省八年级上学期第二次月考数学试卷(解析版) 题型:选择题
关于x的不等式(m+1)x≥m+1的解是x≤1,m的取值范围是 ( )
A.m≤-1 B.m≥-1 C.取任何实数 D.无法确定
查看答案和解析>>
科目:初中数学 来源:2015届浙江省八年级上学期第一次月考数学试卷(解析版) 题型:选择题
如图,∠BAC=90°,AD⊥BC,则图中互余的角有( )

A.2对 B.3对 C.4对 D.5对
查看答案和解析>>
科目:初中数学 来源:2015届湖北省武汉市黄陂区八年级下学期期末数学试卷(解析版) 题型:解答题
如图,在?ABCD中,E是AD上一点,连接BE,F为BE中点,且AF=BF,

(1)求证:四边形ABCD为矩形;
(2)过点F作FG⊥BE,垂足为F,交BC于点G,若BE=BC,S△BFG=5,CD=4,求CG.
查看答案和解析>>
科目:初中数学 来源:2015届辽宁省大连市八年级10月月考数学试卷(解析版) 题型:填空题
如图所示,小亮从A点出发前进l0m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,当他第一次回到出发点A时,一共走了 m.

查看答案和解析>>
科目:初中数学 来源:2015届黑龙江省绥棱县八年级五四制上学期期末考试数学试卷(解析版) 题型:选择题
甲、乙两班学生植树造林,已知甲班每天比乙班多植5棵树,甲班植80棵树所用的天数与乙班植70棵树所用的天数相等,若设甲班每天植树x棵,则根据题意列出的方程是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com