
【题目】如图,一个正比例函数y1=k1x的图象与一个一次函数y2=k2x+b的图象相交于点A(3,4),且一次函数y2的图像与y轴相交于点B(0,—5),与x轴交于点C.
(1)判断△AOB的形状并说明理由;
(2)请写出当y1>y2时x的取值范围;
(3)若将直线AB绕点A旋转,使△AOC的面积为8,求旋转后直线AB的函数解析式;
(4)在x轴上求一点P使△POA为等腰三角形,请直接写出所有符合条件的点P的坐标.
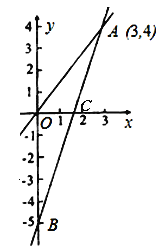
【答案】(1)△AOB是等腰三角形,证明详见解析;(2)x<3;(3)y=-4x+16或y=![]() ;(4) P(5,0)或(-5,0)或(6,0)或(
;(4) P(5,0)或(-5,0)或(6,0)或(![]() ).
).
【解析】
(1)根据A的坐标求得OA和OB的长度即可判断;
(2)根据图象当y1>y2时即y1的函数值大,即对相同的x的值,y1对应的图象的点在上边,根据图象即可写出;
(3)首先根据三角形的面积公式求得OC的长,即可得到C的坐标,利用待定系数法即可求解;
(4)已知等腰三角形POA中的一边OA,分1)OA是底边;2)OA是腰,且A是顶角的顶点;3)OA是腰,且O是顶角的顶点.三种情况进行讨论.
解:(1)OA=![]() =5,则OA=OB,
=5,则OA=OB,
∴△AOB是等腰三角形;
(2)根据图象可以得到:当y1>y2时x<3;
(3)设OC=x,则![]() x×4=8,解得:x=4,
x×4=8,解得:x=4,
则C的坐标是:(-4,0)或(4,0).
设直线AB的解析式是:y=kx+b,当C的坐标是:(-4,0)时,根据题意得:
![]() ,
,
解得: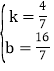 ,
,
则直线的解析式是:y=![]() x+
x+![]() ;
;
当C的坐标是(4,0)时,根据题意得:
![]() ,
,
解得:![]() ,
,
则直线的解析式是:y=-4x+16;
(4)把(3,4)代入y1=k1x得到:3k1=4,
解得:k1=![]() ,
,
当OA是底边时,OA的中点是(![]() ,2),设过OA的中点且与OA垂直的直线的解析式是:y=-
,2),设过OA的中点且与OA垂直的直线的解析式是:y=-![]() x+b,
x+b,
根据题意得:b=![]() ,
,
直线的解析式是:y=-![]() x+
x+![]() ,
,
当y=0时,x=![]() ,
,
则P的坐标是(![]() ,0);
,0);
当OA是腰,O是顶角的顶点时,OP=OA=5,则P的坐标是(5,0)或(-5,0);
当OA是腰,A是顶角的顶点时,AP=AO,则P与O关于x=3对称,则P的坐标是(6,0).
则P的坐标是:(![]() ,0)或(5,0)或(-5,0)或(6,0).
,0)或(5,0)或(-5,0)或(6,0).


科目:初中数学 来源: 题型:
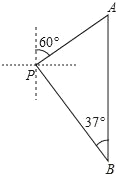
【题目】小亮一家到桃林口水库游玩.在岸边码头P处,小亮和爸爸租船到库区游玩,妈妈在岸边码头P处观看小亮与爸爸在水面划船,小船从P处出发,沿北偏东60°方向划行,划行速度是20米/分钟,划行10分钟后到A处,接着向正南方向划行一段时间到B处,在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米?(精确到1m,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.
(1)点D在边AB上时,证明:AB=FA+BD;
(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请画出图形并直接写出正确结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察如图所示的长方体.
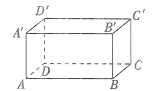
(1)用符号表示下列两棱的位置关系:AB___A′B′,AA′_____AB,D′A′_____D′C′,AD______BC.
(2) A′B′与BC所在的直线是两条不相交的直线,它们_____平行线.(填“是”或“不是”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据生物学研究结果,青春期男、女生身高增长速度呈现如下图规律,由图可以判断,下列说法错误的是( )
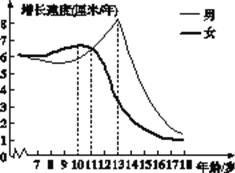
A. 男生在13岁时身高增长速度最快
B. 女生在10岁以后身高增长速度放慢
C. 11岁时男、女生身高增长速度基本相同
D. 女生身高增长的速度总比男生慢
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如下表和图①:
A | B | C | |
笔试 | 85 | 95 | 90 |
口试 | 80 | 85 |
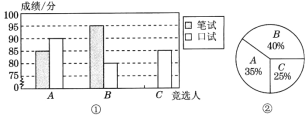
(1)请将表格和图①中的空缺部分补充完整;
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图②(没有弃权票,每名学生只能推荐一人),请计算每人的得票数;
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4∶3∶3的比确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D为直线BC上一动点(点D不与B、C重合)以AD为边作正方形ADEF,使∠DAF=∠BAC,连接CF.
(1)如图1,当点D在线段BC上时,求证:BD=CF;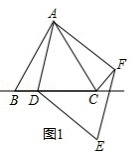
(2)如图2,当点D在线段BC的延长线上,且∠BAC=90°时.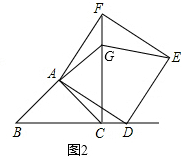
①问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
②延长BA交CF于点G,连接GE,若AB=2 ![]() ,CD=BC,请求出GE的长.
,CD=BC,请求出GE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海边的一段堤岸高出海平面12米,附近的某建筑物高出海平面50米,演习中的某潜水艇在海平面下30米处.
(1)现以海平面的高度为基准,将其记为0米,高于海平面记为正,低于海平面记为负,那么堤岸、附近建筑物及潜水艇的高度各应如何表示?
(2)若以堤岸高度为基准,则堤岸、建筑物及潜水艇的高度又应如何表示?

查看答案和解析>>
科目:初中数学 来源: 题型:
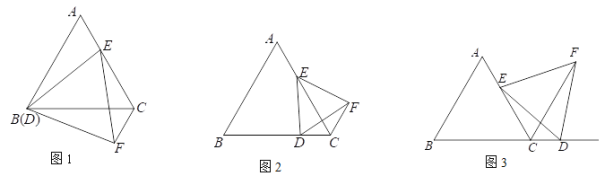
【题目】△ABC是等边三角形,点E在AC边上,点D是BC边上的一个动点,以DE为边作等边△DEF,连接CF.
(1)如图1,当点D与点B重合时,求证:△ADE≌△CDF;
(2)如图2,当点D运动到如图2的位置时,猜想CE、CF、CD之间的数量关系,并说明理由;
(3)如图3,当点D在BC延长线上时,直接写出CE、CF、CD之间的数量关系,不证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com