
����Ŀ������ģ�ͣ�
��������ͼ1��A��B��ֱ��![]() ͬ�Ե��������㣮
ͬ�Ե��������㣮

���⣺��ֱ��![]() ��ȷ��һ��P��ʹPA+PB��ֵ��С��
��ȷ��һ��P��ʹPA+PB��ֵ��С��
����������A����ֱ��![]() �ĶԳƵ�A��������A��B��
�ĶԳƵ�A��������A��B��![]() �ڵ�P����PA+PB=A��B��ֵ��С������֤������
�ڵ�P����PA+PB=A��B��ֵ��С������֤������
ģ��Ӧ�ã�
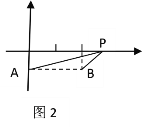
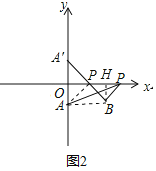
��1����ͼ2,��֪ƽ��ֱ������ϵ��������A��0��-1����B��2��-1��,PΪx����һ����, ��PA+PB��ֵ��Сʱ����P�ĺ�������______����ʱPA+PB����Сֵ��______��
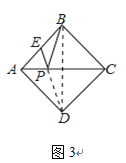
��2����ͼ3��������ABCD�ı߳�Ϊ2��EΪAB���е㣬P��AC��һ����.�������ζԳ��Կ�֪��B��D����ֱ��AC�Գƣ�����BD����PB+PE����Сֵ��______��
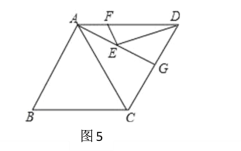
��3����ͼ4,������ABCD�����Ϊ12����ABE�ǵȱ������Σ���E��������ABCD�ڣ��ڶԽ���AC����һ����P����PD��PE����СֵΪ ��
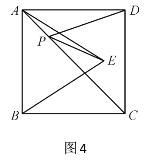
��4����ͼ5,������ABCD�У�AB=8����B=60������G�DZ�CD�ߵ��е㣬��E��F�ֱ���AG��AD�ϵ��������㣬��EF+ED����Сֵ��_______________.
���𰸡���1����P�ĺ������� 1 ����ʱPA+PB����Сֵ��![]() ����2��PB+PE����Сֵ��
����2��PB+PE����Сֵ��![]() ��3�������СֵΪ
��3�������СֵΪ ![]() ����4��EF+ED����Сֵ��
����4��EF+ED����Сֵ��![]()
��������
��1��ȡ��A����x��ԳƵĵ�A��������A��B����x����P����BH��x����H�����OP���õ���P�ĺ����꣬���ݹ��ɶ������A��B���õ��𰸣�
��2����������PB+PE=PD+PE=DE������ADE�У����ݹ��ɶ�����ü��ɣ�
��3�����ڵ�B��D����AC�Գƣ���������BD����AC�Ľ��㼴ΪF�㣮��ʱPD+PE=BE��С����BE�ǵȱ���ABE�ıߣ�BE=AB����������ABCD�����Ϊ12�������AB�ij����Ӷ��ó������
��4����DH��AC����ΪH��AG���ڵ�E����H����AG�ĶԳƵ�ΪF����ʱEF+ED��С=DH����֤����ADC�ǵȱ������Σ���RT��DCH�����ù��ɶ������ɽ�����⣮
��1��ȡ��A����x��ԳƵĵ�A��������A��B����x����P����BH��x����H��
���ʱPA+PB��ֵ��С��
��OA��=OA=1��BH=1��BH��OA����
��OP=PH=1��
���P�������1��
PA+PB=A��B=![]() ��
��
�ʴ�Ϊ��1��2![]() ��
��
��2�����ı���ABCD�������Σ�
��AC��ֱƽ��BD��
��PB=PD��
�������ã�PB+PE=PD+PE=DE��
����ADE�У����ݹ��ɶ����ã�DE=![]() ��
��
��3������BD����AC���ڵ�F��

�ߵ�B��D����AC�Գƣ�
��PD=PB��
��PD+PE=PB+PE=BE����
��������ABCD�����Ϊ12��
��AB=2![]() ��
��
�֡ߡ�ABE�ǵȱ������Σ�
��BE=AB=2![]() ��
��
��������СֵΪ2![]() ��
��
��4����ͼ��DH��AC����ΪH��AG���ڵ�E��
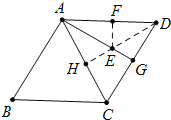
���ı���ABCD�����Σ�
��AB=AD=CD=BC=8��
�ߡ�B=60����
���ADC=��B=60����
���ADC�ǵȱ������Σ�
��AG�����ߣ�
���GAD=��GAC
���H����AG�ĶԳƵ�F��AD�ϣ���ʱEF+ED��С=DH��
��RT��DHC�У��ߡ�DHC=90����DC=6����CDH=![]() ��ADC=30����
��ADC=30����
��CH=![]() DC=4��DH=
DC=4��DH=![]() ��
��
��EF+DE����Сֵ=DH=4![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�Ƶ�C˳ʱ����ת90���õ���EDC������A��D��E��ͬһ��ֱ���ϣ���ACB=20�������ADC�Ķ����ǣ�������

A. 55�� B. 60�� C. 65�� D. 70��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ���������֣��������:
![]() ��һ������������������������ѭ��С�������
��һ������������������������ѭ��С�������![]() ��С��������ȫ��д�������������ǿ�����취������ʾ����.��Ϊ
��С��������ȫ��д�������������ǿ�����취������ʾ����.��Ϊ![]() ������
������![]() ����������Ϊ
����������Ϊ![]() ����
����![]() ��ȥ���������ֺõ��IJ����С�����֣�����
��ȥ���������ֺõ��IJ����С�����֣�����![]() ��С������Ϊ
��С������Ϊ![]() ��
��
��1�����![]() ���������ֺ�С������:
���������ֺ�С������:
��2�����![]() ���������ֺ�С�����֣�
���������ֺ�С�����֣�
��3�����![]() ������������
������������![]() ����������
����������![]() �����
�����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ![]() ����ֱ֪��
����ֱ֪��![]() ��
��![]() �ᣬ
�ᣬ![]() ��ֱ���
��ֱ���![]() ��
��![]() ���㣬��
���㣬��![]() Ϊֱ�Ƕ����ڵڶ�����������
Ϊֱ�Ƕ����ڵڶ�����������![]() ��
��
��1�����![]() �����꣬�����ֱ��
�����꣬�����ֱ��![]() �Ĺ�ϵʽ��
�Ĺ�ϵʽ��
��2����ͼ![]() ��ֱ��
��ֱ��![]() ��
��![]() ����
����![]() ����ֱ��
����ֱ��![]() ��ȡһ��
��ȡһ��![]() ������
������![]() ����
����![]() ����֤��
����֤��![]() ��
��
��3����ͼ![]() ���ڣ�1���������£�ֱ��
���ڣ�1���������£�ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ���߶�
���߶�![]() ��һ�㣬��
��һ�㣬��![]() �����Ƿ����һ��
�����Ƿ����һ��![]() ��ʹ
��ʹ![]() �������
�������![]() �����һ�룿�����ڣ��������
�����һ�룿�����ڣ��������![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AE��BC��E������ABE��AE����ֱ�߷��۵���AEF����AB��2����B��45��������AEF������ABCD�ص����֣���Ӱ���֣������Ϊ�� ��.
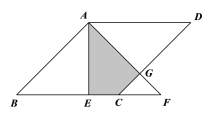
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʮ����й��������ᡱ����2014��10�µ��ڳɶ��ٿ�������20��־Ը�����μ�ij�ֻ᳡�Ĺ�������������8�ˣ�Ů��12��.
��1��������20�������ѡȡһ����Ϊ����Ա����ѡ��Ů���ĸ��ʣ�
��2�����÷ֻ᳡��ij���ֻ�ڼס���������ѡһ�ˣ�����������Ϸ�ķ�ʽ������˭�μӣ���Ϸ�������£��������������ֱַ�Ϊ2��3��4��5���˿���ϴ�Ⱥ����ֳ��·������棬������ȡ2�ţ�����������֮��Ϊż������ײμӣ������Ҳμ�.���������Ϸ��ƽ��������״ͼ���б���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪PA��PB����O�����ߣ�A��B�ֱ�Ϊ�е㣬��OAB=30�㣮
��1����APB=_____��
��2����OA=2ʱ��AP=_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
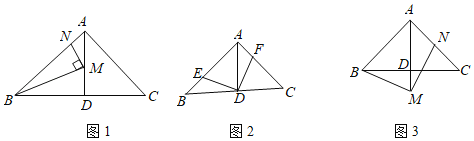
����Ŀ����![]() �У�
��![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
��1����ͼ1����![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �ϣ���
�ϣ���![]() ����
����![]() ��
��![]() ʱ�����߶�
ʱ�����߶�![]() �ij���
�ij���
��2����ͼ2����![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �ϣ���
�ϣ���![]() ����֤��
����֤��![]() ��
��
��3����ͼ3����![]() ��
��![]() ���ӳ����ϣ���
���ӳ����ϣ���![]() ��
��![]() �ϣ���
�ϣ���![]() ����֤��
����֤��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCD��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ���Խ���AC��BD�Ľ���Eǡ����y���ϣ�����D��BC���е�H��ֱ�߽�AC�ڵ�F���߶�DE��CD�ij��Ƿ���x2��9x+18=0�������������������⣺
��1�����D�����ꣻ
��2��������������y=![]() ��k��0����ͼ����H����k=�� ����
��k��0����ͼ����H����k=�� ����
��3����Q��ֱ��BD�ϣ���ֱ��DH���Ƿ���ڵ�P��ʹ�Ե�F��C��P��QΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com