
【题目】如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E.
(1)试判断DE与⊙O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F,若BE=3![]() ,DF=3,求图中阴影部分的面积.
,DF=3,求图中阴影部分的面积.
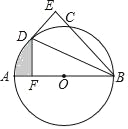
【答案】(1)DE与⊙O相切,理由见解析;(2)阴影部分的面积为2π﹣![]() .
.
【解析】(1)直接利用角平分线的定义结合平行线的判定与性质得出∠DEB=∠EDO=90°,进而得出答案;
(2)利用勾股定理结合扇形面积求法分别分析得出答案.
(1)DE与⊙O相切,
理由:连接DO,
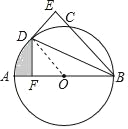
∵DO=BO,
∴∠ODB=∠OBD,
∵∠ABC的平分线交⊙O于点D,
∴∠EBD=∠DBO,
∴∠EBD=∠BDO,
∴DO∥BE,
∵DE⊥BC,
∴∠DEB=∠EDO=90°,
∴DE与⊙O相切;
(2)∵∠ABC的平分线交⊙O于点D,DE⊥BE,DF⊥AB,
∴DE=DF=3,
∵BE=3![]() ,
,
∴BD=![]() =6,
=6,
∵sin∠DBF=![]() ,
,
∴∠DBA=30°,
∴∠DOF=60°,
∴sin60°=![]() ,
,
∴DO=2![]() ,
,
则FO=![]() ,
,
故图中阴影部分的面积为:![]() .
.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC和△AOD是等腰直角三角形,AB=AC,AO=AD,∠BAC=∠OAD=90°,点O是△ABC内的一点,∠BOC=130°.
(1)求证:OB=DC;
(2)求∠DCO的大小;
(3)设∠AOB=α,那么当α为多少度时,△COD是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
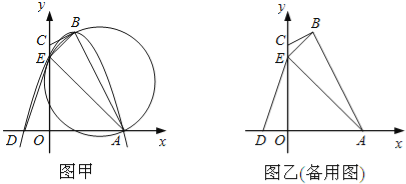
【题目】如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE=![]() ,A(3,0),D(﹣1,0),E(0,3).
,A(3,0),D(﹣1,0),E(0,3).
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由;
(4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE与△ABE重叠部分的面积为s,求s与t之间的函数关系式,并指出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一种密码,将英文26个字舟a,b,c,…,z(不论大小写)依次对应1,2,3,…,26,这26个自然数(见表格),当明码对应的序号x为奇数时,密码对应的序号![]() ,当明码对应的序号x为偶数时,密码对应的序号
,当明码对应的序号x为偶数时,密码对应的序号![]() +12,按下述规定,将明码“love”译成密码是( )
+12,按下述规定,将明码“love”译成密码是( )

A.loveB.rkwuC.sdriD.rewj
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:平行四边形ABCD,求作菱形AECF,使点E、点F分别在BC、AD边上
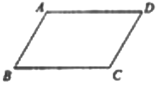
下面是小明设计的尺规作图过程.
作法:如图
① 连接AC;
② 分别以A、C为圆心,大于![]() AC的长为半径作弧,两弧交于M、N两点;
AC的长为半径作弧,两弧交于M、N两点;
③ 连接MN,分别与BC、AD、AC交于E、F、O三点;
④ 连接AE、CF
四边形AECF即为所求
根据小明设计的尺规作图过程
(1)使用直尺和圆规,补全图形:(保留作图痕迹)
(2)完成下面的证明
证明∵AM= ,AN= ,
∴MN是AC的垂直平分线。
( )(填推理的依据)
∴EF⊥AC,OA=OC,
∴平行四边形ABCD
∴AD∥BC
∴∠FAO=∠ECO
在△FAO和△ECO中

∴△FAO≌△ECO
∴OE=OF
又∵OA=OC
∴四边形AECF是平行四边形
( )(填推理依据)
∵EF⊥AC
∴四边形AECF是菱形
( )(填推理依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对给定的一张矩形纸片ABCD进行如下操作:先沿CE折叠,使点B落在CD边上(如图①),再沿CH折叠,这时发现点E恰好与点D重合(如图②)
(1)根据以上操作和发现,求![]() 的值;
的值;
(2)将该矩形纸片展开.
①如图③,折叠该矩形纸片,使点C与点H重合,折痕与AB相交于点P,再将该矩形纸片展开.求证:∠HPC=90°;
②不借助工具,利用图④探索一种新的折叠方法,找出与图③中位置相同的P点,要求只有一条折痕,且点P在折痕上,请简要说明折叠方法.(不需说明理由)
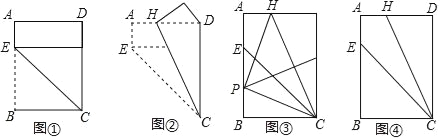
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西安市管理部门对“十一”国庆放假期间七天本市某景区客流变化量进行了不完全统计,数据如下(用正数表示客流量比前一天增加,用负数表示客流量比前一天下降):
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
变化(万人) |
|
|
|
|
|
|
|
请通过计算解决以下问题:
(1)请判断这7天中,哪一天人数最多?哪一天人数最少?
(2)与10月3日相比,10月5日的客流量是上升了还是下降了?
(3)如图9月30日的客流量为1.5万人,据统计平均每人每天消费200元,请问该景区在“十一”七天国庆假期的总收入为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点M,N的坐标分别为(﹣1,2),(2,1),若抛物线y=ax2﹣x+2(a≠0)与线段MN有两个不同的交点,则a的取值范围是( )
A. a≤﹣1或![]() ≤a<
≤a<![]() B.
B. ![]() ≤a<
≤a<![]()
C. a≤![]() 或a>
或a>![]() D. a≤﹣1或a≥
D. a≤﹣1或a≥![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地电话拨号入网有两种收费方式,用户可以任选其一.
计时制:0.05元/分;
包月制:50元/月(限一部个人住宅电话上网).
此外,每一种上网方式都得加收通信费0.02元/分.
(1)某用户某月上网的时间为x小时,请你分别写出两种收费方式下该用户应该支付的费用.
(2)若某用户估计一个月内上网的时间为20小时,你认为采用哪种方式较为合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com